SOLUTION: please help me solve this equation : {{{ x/2

Click here to see ALL problems on Number-Line

Question 263390: please help me solve this equation :

Found 3 solutions by CubeyThePenguin, josgarithmetic, ikleyn:
Answer by CubeyThePenguin(3113)   (Show Source):
You can put this solution on YOUR website!
Multiply both sides by 2(x+4).

x(x+4) > 5(2) + 4(2)(x+4)
x^2 + 4x > 10 + 8x + 32
x^2 - 4x - 42 > 0

The solution is the area outside the quadratic's roots.

Answer by josgarithmetic(39618)   (Show Source):
You can put this solution on YOUR website!

..
..

Answer by ikleyn(52793)   (Show Source):
You can put this solution on YOUR website!
please help me solve this equation :
> +
~~~~~~~~~~~~~

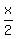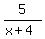            The "solutions" from both @CubeyThePenguin and @josgaritmetic are WRONG.

            Below I brought the correct solution.

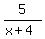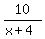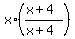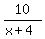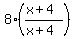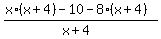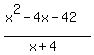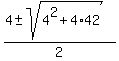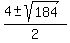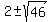Rewrite it equivalently in this form - - 4 > 0 - - 8 > 0 - - > 0 <<<--- now we have common denominator (x+4) > 0 > 0 > 0 The quadratic polynomial in the numerator has the roots = = = . So, the numerator has the roots = = 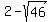-4.782 and = = 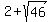8.782. There are three critical points on the number line, = = 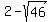-4.782, -4 and = = 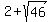8.782. They divide the number line in 4 intervals, from left to right (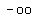,), (,), (,) and ,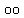). The solution set for the given inequality is the union of the second and the fourth intervals.

Solved.

SOLUTION: please help me solve this equation : {{{ x/2 > 5/(x+4) +4 }}}