Question 263282: A collection of 20 coins made up of only nickels, dimes and quarters has a total value of $3.35. If the dimes were nickels, the nickels were quarters and the quarters were dimes, the collection of coins would have a total value of $2.75. How many quarters are in the original collection?
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let the original number of coins be n, d, q
:
Write an equation for each statement:
:
"A collection of 20 coins"
n + d + q = 20
:
"made up of only nickels, dimes and quarters has a total value of $3.35."
.05n + .10d + .25q = 3.35
:
"If the dimes were nickels, the nickels were quarters and the quarters were dimes, the collection of coins would have a total value of $2.75."
.25n + .05d + .10q = 2.75
:
Multiply the above equation by 4, subtract from the 1st equation
1n + 1d + 1q = 20
1n +.2d +.4q = 11
---------------------subtraction eliminates n
.8d + .6q = 9
:
Multiply the 2nd equation by 20, subtract the 1st equation
1n + 2d + 5q = 67
1n + 1d + 1q = 20
-----------------------subtraction eliminates n again
d + 4q = 47
:
Use elimination again on the these two, 2 unknown equations
Multiply the above equation by 4, multiply the 1st by 5, subtract it
4d + 16q + 188,
4d + 3q = 45
----------------------subtraction eliminates d, find q
13q = 143
q = 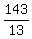
q = 11
:
How many quarters are in the original collection?
11 quarters originally
|
|
|