Question 263246: How do I start to solve this problem? I have tried to solve but I am so confused.
ACTIVITY 1: ISBNS AND THE CHECK DIGIT (20 points)
Each activity in this text is designed to either enhance your understanding of the topics of the preceding chapter, provide you with a mathematical extension of those topics, or both. The activities can be undertaken by one student, but they are better suited for a small group project. Occasionally it is only through discussion that different facets of the activity become apparent. For material related to this activity, visit the text website at www.mhhe.com/streeter. Have you ever noticed the long number, usually accompanied by a bar code, that can be found on the back of a book? This is called the International Standard Book Number (ISBN). Each book has a unique ISBN, which is 10 digits in length. The most common form for an ISBN is X-XX-XXXXXX-X. Each ISBN has four blocks of digits.
• The first block of digits on the left represents the language of the book (0 is used to represent
English). This block is usually one digit in length.
• The second block of digits represents the publisher. This block is usually two or three
digits in length.
• The third block of digits represents the number assigned to the book by the publishing
company. This is usually five or six digits in length.
• The fourth block consists of the check digit.
For the purposes of this document, we will consider the ISBN 0-07-229654-2.
The digit of most interest is the final digit, the check digit. When an ISBN is entered
into a computer, the computer looks at the check digit to make certain that the numbers
were properly entered. We will look at the algorithm used to generate the check digit.
Activity
I. To determine the check digit for the ISBN of a text, follow these steps.
1. Multiply each of the nine assigned digits by a weighted value. The weighted values
are 1 for the first digit from the left, 2 for the second digit, 3 for third digit, etc. In our
case, we have
1 • 0 + 2 • 0 + 3 • 7 + 4 • 2 + 5 • 2 + 6 • 9 + 7 • 6 + 8 • 5 + 9 • 4 = 211
2. In mathematics, we occasionally are interested in only the remainder after we do
division. We refer to the remainder as the modular (or mod) of the divisor. The ISBN
uses (mod 11) to determine the check digit.
211 ÷ 11 = 19 with a remainder of 2. We say 211 = 2 (mod 11)
That is how we get the 2 in the ISBN 0-07-229654-2.
II. If we are given an ISBN and we want to check its validity, we can follow a similar
algorithm.
1. Multiply each of the 10 digits by a weighted value. The weighted values are still 1 for
the first digit from the left, 2 for the second digit, etc., but we also multiply 10 times
the tenth (check) digit.
In our case, we now have
1 • 0 + 2 • 0 + 3 • 7 + 4 • 2 + 5 • 2 + 6 • 9 + 7 • 6 + 8 • 5 + 9 • 4 + 10 • 2 = 231
2. For any valid ISBN, the result will have a remainder of zero when divided by 11. In
other words, we will have 0 (mod 11). Note that 231 ÷ 11 = 21.
Determine whether each of the following is a valid ISBN.
0-07-038023-6
0-15-249584-2
0-553-34948-1
0-07-000317-3
For those numbers above that are valid, go on-line and find the books to which they refer.
Answer by mducky2(62)   (Show Source): (Show Source):
You can put this solution on YOUR website! This looks complicated, but it's actually pretty simple. You just want to figure out which of the 4 IBSNs are valid. There are 2 ways to figure out whether an ISBN is valid, and you can use either one.
First Strategy
Let's use the first strategy with 0-07-038023-6. Except for the last digit, we're supposed to multiply all the numbers with their place in the ISBN, then add these answers up to a grand total. The 1st number is 0, the 2nd number is 0, the 3rd number is 7, and so on.
So, for the first three numbers, we'd get 1*0, 2*0, and 3*7. To do that for all the numbers looks like this:
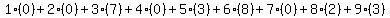
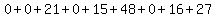

Now we're supposed to divide that number by 11, and look at the remainder. Let's divide 127 by 11.
 
That means the remainder is 6 . Looking at the original ISBN, 0-07-038023-6, we see that the last number is 6. That means that the ISBN is valid!
Second Strategy
Let's use the second strategy with 0-15-249584-2. Including the last digit, we're supposed to multiply all the numbers with their place in the ISBN, then add everything to a grand total. It's basically the first strategy, plus the last digit times 10.
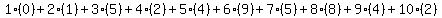
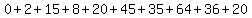
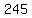
Now we're supposed to divide that number by 11. If it's a valid number, it shouldn't have any remainder.
 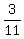
Hmm. There is a remainder. It looks like this one isn't valid.
That should help you get started. You can use either one of these strategies for the last two numbers, 0-553-34948-1 and 0-07-000317-3. Let me know if you need more help with the last two problems.
|
|
|