Question 262522: if the total distance from city A to city B to city C and back to city A is 1400 miles, and it is 600 miles between two cities that are furthest apart, what are the two distances between cities?
Answer by drk(1908)   (Show Source): (Show Source):
You can put this solution on YOUR website! Draw isosceles triangle ABC, where a is bottom left, B is bottom right and C is top vertex. Let AB = 600, this means we have 800 miles left over.
The other distances must add to 800, but neither one can be 600. It appears we have many options.
Suppose
distance 1 is AB = 600
distance 2 is BC = x
distance 3 is CA = y
---
by triangle inequality theorem
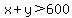
also

If x = 599, then y = 201
If x = 500, then y = 300
if x = 450, then y = 350
and so on
If x = 201, then y= 599
---
200 < x < 600 u y < 800-x
|
|
|