|
Question 262455: I am trying to help my niece with her homework and I need step-by-step instructions on how to use substitution to solve a system of equations.
Example:
2x + 3y = 5
4x - 9y = 9
Thanks for any help that you can share!!
Found 4 solutions by stanbon, scott8148, Edwin McCravy, richwmiller:
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! I am trying to help my niece with her homework and I need step-by-step instructions on how to use substitution to solve a system of equations.
Example:
2x + 3y = 5
4x - 9y = 9
------
These are optional steps. There are many ways to
proceed.
----
1st: Solve the 1st equation for "x", as follows:
2x + 3y = 5
2x = -3y + 5
x = (-3y+5)/2
---------------------------
2nd: Substitute for "x" in the 2nd original equation and solve for "y":
4[(-3y+5)/2] - 9y = 9
2(-3y+5) - 9y = 9
-6y + 10 - 9y = 9
-15y = -1
y = 1/15
----------
Since x = (-3y+5)/2, x = (-3(1/15)+5)/2,
x = [(-1/5)+5/2 = (24/5)/2 = 12/5
------------------------
Final Answer: y = -1/3 when x = 12/5
=======================================
Cheers,
Stan H.
Answer by scott8148(6628)   (Show Source): (Show Source):
You can put this solution on YOUR website! the "trick" is to substitute an equivalent value to get an equation with only one variable
look for a simple ratio between the terms of the SAME variable in the different equations
___ eg. the x term in the first equation is 2, while the x term in the second equation is 4
___ a simple ratio of 1:2
subtracting 3y in the first equation gives ___ 2x = 5 - 3y
in the second equation, the 4x term can be thought of as 2(2x)
so substituting the equivalent value of 2x from the first equation gives ___ 2(5 - 3y) - 9y = 9
distributing the 2 ___ 10 - 6y - 9y = 9 ___ 1 = 15y ___ 1/15 = y
substituting the value of y into the first equation ___ 2x + 3(1/15) = 5 ___ 2x = 72/15 ___ x = 36/15 = 12/5
Answer by Edwin McCravy(20060)   (Show Source): (Show Source):
You can put this solution on YOUR website! 
Substitution is the worst way to solve a system which
does not have any letters with coefficient of 1 or -1.
Such systems are much easier solved by elimination.
However, since you specified to do it by substitution,
I will do so, but it will be much more difficult, as
it will involve lots of work with fractions. Here goes:
Solve the first equation for x


 Substitute
Substitute 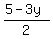 for for 

 Cancel the 2 into the 4 and get a 2 where the 4 is
Cancel the 2 into the 4 and get a 2 where the 4 is
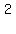 
 Distribute to remove the parentheses:
Distribute to remove the parentheses:
 Combine like terms:
Combine like terms:
 Add -10 to both sides:
Add -10 to both sides:
 Divide both sides by
Divide both sides by 
 Cancel the
Cancel the  's, and simplify the right side 's, and simplify the right side

 Now we substitute
Now we substitute  for for  into into

 Cancel the 3 into the
Cancel the 3 into the 

 Simplify the compound fraction by multiplying
the numerator and denominator by the LCD of 5
Simplify the compound fraction by multiplying
the numerator and denominator by the LCD of 5
 Distribute the 5 into the parentheses, and write 10 for the
denominator
Distribute the 5 into the parentheses, and write 10 for the
denominator  : :
 Write 25 for 5*5 and cancel the 5's in the second
term on top:
Write 25 for 5*5 and cancel the 5's in the second
term on top:


 We reduce the fraction:
We reduce the fraction:
 So the solution is
So the solution is  , ,  But that is by far the hardest way to solve a
system of equations which has none of the terms
x, -x, y, or -y. The easist way would be the
elimination method.
Edwin
But that is by far the hardest way to solve a
system of equations which has none of the terms
x, -x, y, or -y. The easist way would be the
elimination method.
Edwin
Answer by richwmiller(17219)   (Show Source): (Show Source):
You can put this solution on YOUR website! Edwin is right. Substitution is the worst way to solve it.
Elimination is the way to go.
Just so you see how much easier it is with elimination.
This system begs to be done by elimination.
9 is a multiple of 3 and 4 is a multiple of 2.
Sow e have several choices.
I choose multiply first by 3 and add
6x+9y=15
4x-9y=9
add
10x=24
x=24/10 or 12/5 or 2.4
we could just plug 12/5 into any equation and solve for y
but we'll solve using elimination too!
multiply first equation by 2
4x+6y=10
4x-9y=9
subtract
15y=1
y=1/15
x=12/5
(12/5,1/15)
These equations were begging for elimination.
|
|
|
| |