 base is 2 for all
I think you meant
base is 2 for all
I think you meant
 In algebra.com triple bracket notation, that's written
In algebra.com triple bracket notation, that's written
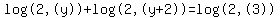
 Anyway,
Anyway,
 Use the principle of logs:
Use the principle of logs:  to rewrite the left side:
to rewrite the left side:
 Now use the principle that if
Now use the principle that if  then
then




 ;
; 
 ;
;  Now we must dicard the answer
Now we must dicard the answer  ,
because if we were to substitute that into
the original equation, the first term would be
,
because if we were to substitute that into
the original equation, the first term would be
 and logs of negative numbers
are not defined as real numbers. So the only
solution is
and logs of negative numbers
are not defined as real numbers. So the only
solution is  Edwin
Edwin