|
Question 261136: I need help on how to Factor the Polynomial. I asked a similar question earlier, but the answer was wrong and I didnt understand how it was worked. Could someone go through and answer this question for me please?
Factor the Polynomial:
12x^8-18x^4y^5-10x^4y^5+15y^10
Wouldn't I combine the like terms of xy first?
Thank you
Found 2 solutions by richwmiller, jsmallt9:
Answer by richwmiller(17219)   (Show Source):
You can put this solution on YOUR website! If you can't factor it how do you know the answer was wrong? Are you holding back?
Especially since you said you didn't understand how it was worked.
Answer by jsmallt9(3758)  (Show Source):
You can put this solution on YOUR website!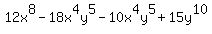 
The middle two terms are like terms so they could be combined. But doing so actually makes the factoring more difficult. (When a problem gives you an unsimplified expression, there is probably a reason.)
When factoring, always start with the Greatest Common Factor (GCF). Unfortunately the GCF here is 1 (which we rarely factor out).
After the GCF, try any and all factoring techniques you know: factoring with patterns, trinomial factoring, factoring by grouping and factoring by trial and error of the possible rational roots. Your expression, with four terms, has too many terms for any of the common patterns and it has too many terms for trinomial factoring. (However, if we did combine the middle two terms we could then use this technique.) Since factoring by trial and error is tedious we will use it as a last resort. So we are left with factoring by grouping.
When factoring by grouping, I like to change any subtractions to additions. When the expression is all additions you can change the order and grouping of the terms freely and this is something that can be quite helpful. It also helps with proper handling of minus signs. So I am going to rewrite your expression as additions:
To factor by grouping you look for pairs of factors that have a GCF between them. This may require rearranging the terms. In your expression the first two terms have a GCF of 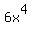 and the last two terms have a common factor of  so initially we do not need to rearrange the terms. We factor out each pair's GCF:
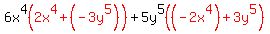
Now, if we're lucky the "non-GCF" factors (in red) of each pair will be the same. Our "non-GCF" factors are not the same. But... they are negatives of each other! So if we factor out a -1 from one of them, we will get a match:
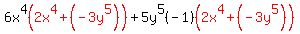
which simplifies to:
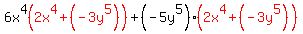
Now we have matching "non-GCF" factors! And we can factor them out. (Note where the non-red parts of the above expression end up in the factored expression.)
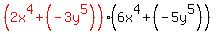
If you decide to combine the middle terms you get:
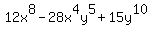
On this expression we could use trinomial factoring. But there are many, many possible combinations to check because there are many, many ways to factor both 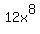 and 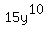 and only one of these combinations actually makes the middle term work out to be  . (You can see the correct combination of factors in the answer we found when factoring by grouping.) In this case factoring by grouping, although not easy, was easier than trinomial factoring. And this is why the expression was unsimplified to begin with.
|
|
|
| |
