SOLUTION: could anybody please help me evaluate this example 1/3logbase7^125+log base7 ^0.2 - log base 7 ^49

Algebra ->  Logarithm Solvers, Trainers and Word Problems -> SOLUTION: could anybody please help me evaluate this example 1/3logbase7^125+log base7 ^0.2 - log base 7 ^49      Log On


   

Question 261038: could anybody please help me evaluate this example 1/3logbase7^125+log base7 ^0.2 - log base 7 ^49
Answer by jsmallt9(3758) About Me  (Show Source):
You can put this solution on YOUR website!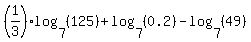
%281%2F3%29log%287%2C+%28125%29%29+%2B+log%287%2C+%280.2%29%29+-+log%287%2C+%2849%29%29
I don't know of a calculator that can calculate base 7 logarithms. So we have two choices:
  • See if the base 7 logarithms can be solved "by hand". Logarithms can be solved by hand if the arguments are powers of the base.
  • Change the base of the logarithm from 7 to a base our calculator knows (like base 10 or base e (aka natural) logarithms).

I will do it both ways.

1) By hand.
At first, the first two logarithms do not appear to be logarithms we can do by hand because 125 and 0.2 are not powers of 7. But we can manipulate these two logarithms using the properties of logarithms and after the manipulation we may have logs of powers of 7.

One property of logarithms, q%2Alog%28a%2C+%28p%29%29+=+log%28a%2C+%28p%5Eq%29%29, allows us to move a coefficient (number in front) into the argument as an exponent of the argument. We can use this on the first logarithm to move the 1/3:
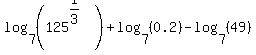
log%287%2C+%28125%5E%281%2F3%29%29%29+%2B+log%287%2C+%280.2%29%29+-+log%287%2C+%2849%29%29
Since 1/3 as an exponent is cube root and since the cube root of 125 is 5 this simplifies to:
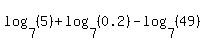
log%287%2C+%285%29%29+%2B+log%287%2C+%280.2%29%29+-+log%287%2C+%2849%29%29
The first two logs still do not look like we can do them by hand. But there is another property we can use, log%28a%2C+%28p%29%29+%2B+log%28a%2C+%28q%29%29+=+log%28a%2C+%28p%2Aq%29%29, which allows us to combine the sum of two logs of the same base into one. Using this property on the first two logs we get:
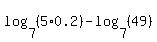
log%287%2C+%285%2A0.2%29%29+-+log%287%2C+%2849%29%29
Since 5*0.2 is 1 this simplifies to:
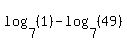
log%287%2C+%281%29%29+-+log%287%2C+%2849%29%29
We now have two logarithms whose arguments are powers of the base! Since 7%5E0+=+1 and 7%5E2+=+49, these logarithms are 0 and 2, respectively:
0+-+2
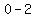
which is -2.

2) By changing the base.
The formula for changing the base is:
log%28a%2C+%28x%29%29+=+log%28b%2C+%28x%29%29%2Flog%28b%2C+%28a%29%29
In this problem we want to change the base from 7 to 10 (or e). So the formula for this would be:
log%287%2C+%28x%29%29+=+log%28%28x%29%29%2Flog%28%287%29%29
or
log%287%2C+%28x%29%29+=+ln%28x%29%2Fln%287%29
Using the first one on the three logarithms we get:

Now we can get out our calculators and find all these logarithms:

And if we use our calculators to simplify all this we should get -2 (or, since all these decimals are just decimal approximations for the real logarithms, something very, very close to -2).

Note: If you use convert to natural logs instead of base 10 logs (using log%287%2C+%28x%29%29+=+ln%28x%29%2Fln%287%29), you still get an answer of -2 (or some decimal very, very close to it).