Question 257306: I need help with this one equation. Here is the question. The price you pay for a box of donuts varies linearly with the number of donuts in the box. For five donuts it costs 1.15, and for eleven it costs 2.35. I can't figure out the equation. Help me please!
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! You are told that the price of the box varies linearly with the number of donuts. This means that if you were to graph ordered pairs of the form (number-of-donuts, price) the points would form a line. So the equation we want is the equation of a line.
To find the equation of a line, you generally need the slope of the line and at least one point on the line. The problem does not give you the slope of the line. But it does give you two ordered pairs: (5, 1.15) and (11, 2.35). And we can find the slope from two ordered pairs using the slope formula:

Inserting our coordinates into this we get:

Since we don;t usually like to have decimals in fractions, I'll multiply the top and bottom by 10 to get rid of the decimal:

which reduces to:

Now we have the slope and two points on the line. There are several ways to get the equation for this line from this information. The most direct way is to use the Point-Slope form:

Inserting our values into this form (using either point, it makes no difference) we get:

This is the equation of the desired line. However, one often prefers to write the equation in either Slope-Intercept form or Standard form. So I will transform this into these forms. First I'll multiply out the right side:

which simplifies to:

Adding 1.15 to each side gives us:

which is Slope-Intercept form. For Standard form, we add 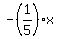 to each side: to each side:

Since Standard form requires no fractions or decimals and a positive leading coefficient, I am going to multiply both side by -20 (which will take of all these issues).
If you don't see how -20 will fix everything all at once, then just take care of one issue at a time. The coefficient of x needs to be a positive integer, the coefficient of y and the constant on the right side need to be integers, too. We can make the coefficient of x positive by multiplying both sides by -1. We can make the coefficient of x an integer by multiplying both sides by 5. The coefficient of y was and should still be an integer after these two steps. The constant on the right, after the first two steps above should be -0.75. We can make this an integer by multiplying both sides by 4.
Back to multiplying both sides by -20:

which simplifies to:

which is Standard form.
|
|
|