Question 256355: i'm doing business algebra online in college, and we're now talking about continuous compound interest. The formula i'm struggling with is the Pert formula. I'm stuck on how to solve a problem when i know what the P, r and t is, but what is the e for? I've never figured out how to come up with the same answer as my study guide example.
For example: Use the continuous compound interest formula to find the indicated value. A=$7,700; r=8.78%; t=10 years; P=? P=_______(round to two decimal places as needed).
I look forward to getting a reply back soon. Hopefully I will get this figured out soon. Thank you.
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! with continuous compounding formula, you get:

f = future value
p = present amount
r = annual interest rate
t = number of years
the e is the symbol for the scientific constant of 2.718281828...
This is an irrational number (never ending non repeating fractional part).
It's called Napier's constant.
the formula for the base of e to an exponent is  where x is the exponent. where x is the exponent.
the inverse formula of  is equal to is equal to  which means the natural log of x. which means the natural log of x.
the basis definition of  is: is:
 if and only if if and only if  . .
this is nothing more than your normal logarithm functions except you have a base of e.
It's no different than the statement:
 if and only if if and only if 
for example:
let x = 3
{y = 10^3}}} = 10*10*10 = 1000
the statement becomes:
 if and only if if and only if  . .
you can confirm that  by using your calculator and taking the log of 3. by using your calculator and taking the log of 3.
you will get 1000.
the base e is nothing more than another base to work with.
In your problem, here's how you would work it.
formula is  . .
you are given:
p = $7,700
r = 8.78%
t = 10 years
first thing you need to do is take all the dollar signs and commas out of p to get:
p = 7700
next thing you need to do is divide 8.78% by 100% to get .0878.
in the formula, you need to work with the rate, not the percent.
since r is an innual interest rate already, you do not need to adjust it any further.
since t is already specified in years, you do not need to adjust it any further.
plug these values into your formula to get:
 becomes becomes

simplify to get:

use your calculator to get 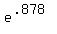 = 2.406082726 = 2.406082726
alternatively, you can substitute the constant of 2.718281828 to get:

solve for f to get:
f = 18526.83699
that's equivalent to $18,526.84.
for some good examples of continuous compounding, check out the web.
do a search on "continuous compounding".
one such website is http://moneychimp.com/articles/finworks/continuous_compounding.htm
It has a calculator that lets you calculate different numbers and see the effect of continuous compounding compared to discrete compounding such as yearly, monthly, daily, and hourly.
It also has a box where you can put in the number of time periods you want.
|
|
|