SOLUTION: One page is missing from a book(that page has two sides,so 2 page numbers).Now the sum of the pages in that book is 8. What are the missing page numbers? Can you help me out the co

Suppose the book originally had n pages

Then the sum of the page numbers originally was 

Suppose page number k and k+1 were torn out. So











Multiply both sides by 2





For that to have a rational solution,
its discriminant must be a perfect square.

Discriminant = 







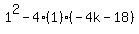
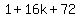
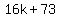All perfect squares end with 1, 4, 5, 6, or 9

Therefore the number to which 73 is added,
namely 16k, in order to get a perfect square 
must end in 8, 1, 5, or 3

That number is 16k, and all multiples of 16 
end in an even digit
 
So 16k must end in 8, the smallest multiple of 16 
that ends in 8 is 48 which is 16*3

so the smallest such value is k=3

That gives the solution as page k = 3 and page k + 1 = 4

So the pages numbers remaining in the book are

pp. 1,2, and 5 and their sum is 8. It really wasn't a "book",
but was only a leaflet!

Edwin