Question 254218: Six cups and saucers come in pairs: there are two cups and saucers which are red, two white, and two with stars on. If the cups are placed randomly onto the saucers (one each), find the probability
that no cup is upon a saucer of the same pattern.
Answer by Edwin McCravy(20054)   (Show Source): (Show Source):
You can put this solution on YOUR website! Six cups and saucers come in pairs: there are two cups and saucers which are red, two white, and two with stars on. If the cups are placed randomly onto the saucers (one each), find the probability
that no cup is upon a saucer of the same pattern.
To place them all successfully, there are two types
of ways of placing them:
An example of 1st type
Saucers R R W W S S
Cups W W S S R R
Example of 2nd type
Saucers R R W W S S
Cups W S R S R W
So we have to consider each type of choice.
For type 1 cases only.
There are 4 ways to place the 1st red cup. Having done that,
there is 1 way to place the 2nd red cup. Having done that,
there are 2 ways to place the 1st white cup. Having done that,
there is 1 way to place the 2nd white cup. Having done that,
there are 2 ways to place the 1st starred cup. Having done that,
there is 1 way to place the 2nd starred cup.
Therefore there are 4*1*2*1*2*1 or 16 ways to place the cups successfully
in a configuration like Type 1.
Example of 2nd type
Saucers R R W W S S
Cups W S R S R W
For type 2 cases only:
There are 4 ways to place the 1st red cup. Having done that,
there are 2 ways to place the 2nd red cup. Having done that,
there are 3 ways to place the 1st white cup. Having done that,
there are 2 ways to place the 2nd white cup. Having done that,
there are 2 ways to place the 1st starred cup. Having done that,
there is 1 way to place the 2nd starred cup.
Therefore there are 4*2*3*2*2*1 or 96 ways to place the cups successfully
in a configuration like Type 2.
So there are a total of 16 + 96 or 112 ways to place the
cups successfully.
----------------------
To place all the cups, regardless of whether successfully or unsuccesfully:
There are 6 ways to place the 1st red cup. Having done that,
there are 5 ways to place the 2nd red cup. Having done that,
there are 4 ways to place the 1st white cup. Having done that,
there are 3 ways to place the 2nd white cup. Having done that,
there are 2 ways to place the 1st starred cup. Having done that
there is 1 way to place the 2nd starred cup.
Therefore there are 6*5*4*3*2*1 or 720 ways to place the cups any
old way.
The probability is therefore 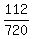 or or 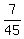 Edwin
Edwin
|
|
|