We break 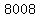 down into a product of prime factors
down into a product of prime factors
 Every perfect square contains exactly an even number of each
of its prime factors. The product above needs a minimum of one
more
Every perfect square contains exactly an even number of each
of its prime factors. The product above needs a minimum of one
more  , one more
, one more  , one more
, one more  , and one more
, and one more  to have an
even number of each of the prime factors 2,7,11,and 13.
That is, it needs to be multiplied by
to have an
even number of each of the prime factors 2,7,11,and 13.
That is, it needs to be multiplied by 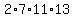 or
or  Thus if n =
Thus if n =  , we have
, we have
 Edwin
Edwin