Question 253894: I am having trouble with a function table.
x Input y is the output #t
x / y
0 / -15
1 / -7
2 / 1
3 / 9
4 / 17
5 / 25
Part A
Write the equation that show how to determine the value of y for any value of x.
Answer_______________ y=
Part B
Use the equation to find the corresponding y-values for x = 6, 7, and 8.
Answer__________33, 41, 49_____________
I was able to see that the values in the y column were increasing by 8
from one line to the next. So I am quite sure that my part b answer is
correct. The only problem is that I couldn't figure out the rule to
create the equation. I was trying to multiply, and subtract and add numbers
and I just couldn't get it.
Please help if you can.
Found 2 solutions by drk, jim_thompson5910:
Answer by drk(1908)   (Show Source): (Show Source):
You can put this solution on YOUR website! You are right in that the slope, m, is 8.
We use Y = mx + b as
Y = 3x + b.
Pick a point (0,-15) to get
-15 = 3*0 + b
Solve for b to get
b = -15
The equation is
Y = 8x - 15
Place (6,7,8) in for x to get
33, 41,,49.
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! a) You are correct in saying that each value is increasing by 8. Since this increase is constant (ie doesn't change), this means that we have a linear equation. So these points form a straight line. Recall that we only need two points to find the equation of the line. So let's use the first two points (0,-15) and (1,-7). You can use any two points.
First let's find the slope of the line through the points ) and and )
Note: ) is the first point is the first point ) . So this means that . So this means that  and and  . .
Also, ) is the second point is the second point ) . So this means that . So this means that  and and  . .
 Start with the slope formula. Start with the slope formula.
 Plug in Plug in  , ,  , ,  , and , and 
 Subtract Subtract  from from  to get to get 
 Subtract Subtract  from from  to get to get 
 Reduce Reduce
So the slope of the line that goes through the points ) and and ) is is 
Now let's use the point slope formula:
 Start with the point slope formula Start with the point slope formula
 Plug in Plug in  , ,  , and , and 
 Rewrite Rewrite 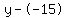 as as 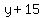
 Distribute Distribute
 Multiply Multiply
 Subtract 15 from both sides. Subtract 15 from both sides.
 Combine like terms. Combine like terms.
So the equation that goes through the points ) and and ) is is 
Notice how the graph of  goes through the points goes through the points ) and and ) . So this visually verifies our answer. . So this visually verifies our answer.

Graph of  through the points through the points ) and and )
------------------------------------------------------------------------------
b)
Now to find the y values at x=6, 7, and 8, just plug them in to get:
x=6: 
x=7: 
x=8: 
So the corresponding y values for x=6, 7, and 8 are y=33, 41, and 49 respectively. Take note that 33 is 8 more than 25 (the y value for x=5), 41 is 8 more than 33, and 49 is 8 more than 41. So this supports our answer.
|
|
|