Question 253630: For p(x)= 4x^5 + 4x^4 + 25x^3 - 56x^2 - 74x - 20
a. Factor into linear and irreducible quadratic factors
b. Factor completely
c. Find all zeros
Answer by drk(1908)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here is pour problem:
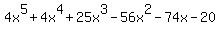
To factor I would first apply: P, N, I using the following table:
P . . . . . N . . . . I
1 . . . . .4 . . . . .0
we have a couple other choices as
P . . . . . N . . . . I
1 . . . . . 2 . . . . 2
1 . . . . . 0 . . . . 4.
We must have a positive root somewhere. Now I turn to P / Q.
The factors of 20 = 1, 2, 4, 5, 10, 20
The factors of 4 = 1, 2, 4.
P/Q means each numerator over each denominator as:
1, 1/2, 1/4, 2, 4, 5, 5/2, 5/4, 10, 5, 2.5, 20.
Through trial and error, we get X = 2, x = -1/2, x = -1/2
By synthetic division
2 [4 . . .4 . . .25 . . . -56 . . . -74 . . . -20]
. 4 . . .12 . . .49 . . .42 . . . . 10 . . .r = 0
-1/2 . [4 . . .12 . . .49 . . .42 . . . . 10]
. . . .4 . . .10 . . .44 . . .20 . . . r = 0]
-1/2 . [4 . . .10 . . .44 . . .20]
. . . 4 . . . 8 . . . 40 . . .r = 0
We have the quadratic function of
4x^2 + 8x + 40
--
part a: Linear and irreducible.
Using quadratic
4x^2 + 8x + 40
becomes
(2x - (-4+13i))*(2x - (-4-13i))
so, we have
(x-2)(2x+1)*(2x+1)*(2x - (-4+13i))*(2x - (-4-13i))
--
part b: factor completely
To me a and b are the same:
(x-2)(2x+1)*(2x+1)(2x - (-4+13i))(2x - (-4+13i))
--
part c: all zero's
X = 2, -1/2, -1/2, (-4 + 13i)/2, (-4 - 13i)/2
|
|
|