|
Question 253258: Need to turn this into standard form...
4x^2+4y^2-24+16y-100=0
4x^2+4y^2+16y=124
4x^2+4y^2+16Y+(1/2 of 16 =8^2=64)=124
4x^2 +4y^2+16y+64-64=124-64
4x^2 + 4y^2+16y=64
4x^2+ (2y+4)^2=64 or 8^2
I know this is not right but i do not know what to do.
Found 2 solutions by jim_thompson5910, Edwin McCravy:
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website!  Start with the given equation. Start with the given equation.
 Combine like terms. Combine like terms.
 Add 124 to both sides. Add 124 to both sides.
 Group the 'y' terms (ie any terms that have a 'y' in them) Group the 'y' terms (ie any terms that have a 'y' in them)
 From that group alone, factor out the GCF 4 From that group alone, factor out the GCF 4
Take half of the 'y' coefficient 4 and square it to get  . Add AND subtract this value inside the parenthesis (so the equation isn't changed) . Add AND subtract this value inside the parenthesis (so the equation isn't changed)
 Add AND subtract the value 4 inside the parenthesis Add AND subtract the value 4 inside the parenthesis

 Inside the parenthesis, group the first three terms. Inside the parenthesis, group the first three terms.
 Factor Factor 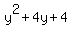 (which is a perfect square) to get (which is a perfect square) to get 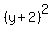
 Distribute. Distribute.
 Add 16 to both sides. Add 16 to both sides.
 Combine like terms. Combine like terms.
 Factor the GCF 4 from the left side. Factor the GCF 4 from the left side.
 Divide both sides by 4. Divide both sides by 4.
 Reduce. Reduce.
Take note that we can write  as as  and and 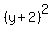 as as 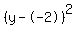 . Also, we can write . Also, we can write  as as 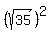 . So the last equation then becomes . So the last equation then becomes

which is in the form  (which is a circle) where (which is a circle) where  , ,  , and , and  . Recall that (h,k) is the center. So the center is (0,-2). Also, the radius is 'r' which means that the radius is . Recall that (h,k) is the center. So the center is (0,-2). Also, the radius is 'r' which means that the radius is 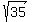 units. units.
===========================================================
Answer:
So the standard form of the equation  is is  which is a circle with radius of which is a circle with radius of 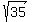 units and a center at (0,-2). units and a center at (0,-2).
Note: your teacher will probably want a simplified answer. So s/he will probably want the answer of  (since it's much cleaner looking). If you want to verify the answer, simply graph the two conic sections and you'll find that they are the same conic section. (since it's much cleaner looking). If you want to verify the answer, simply graph the two conic sections and you'll find that they are the same conic section.
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
You can put this solution on YOUR website! 


First of all notice that every term is divisible by 4,
so let's divide every term by 4:
 Let's add 31 to both sides:
Let's add 31 to both sides:
 Let's complete the square of the last two terms
Let's complete the square of the last two terms 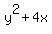 on the left side. We take the coefficient of y, which is 4,
multiply it by
on the left side. We take the coefficient of y, which is 4,
multiply it by  , getting 2, then we square 2, and , getting 2, then we square 2, and
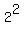 is 4, so we add is 4, so we add 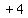 to both sides: to both sides:
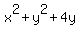   Let's put parentheses around the last three terms on the left
side and combine the terms on the right:
Let's put parentheses around the last three terms on the left
side and combine the terms on the right:
 Now factor the trinomials in the parentheses:
Now factor the trinomials in the parentheses:
 That can be written as
That can be written as
 In fact you could have skipped the step before that.
The standard form for a circle is
In fact you could have skipped the step before that.
The standard form for a circle is
 Since you didn't have to complete the square on the
x term, because you only had an
Since you didn't have to complete the square on the
x term, because you only had an  term and
no x-term, then to get it in the standard form you
have to write term and
no x-term, then to get it in the standard form you
have to write  as as  to have the
standard form, so the answer is to have the
standard form, so the answer is

 is the equation of a circle
which has center (h,k) and radius r
is the equation of a circle
which has center (h,k) and radius r
 is the equation for a circle which has center
(0,-2) and radius
is the equation for a circle which has center
(0,-2) and radius 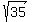 which is about 5.92
and has this graph: which is about 5.92
and has this graph:
 ----------------------------------------------
Are you sure there wasn't supposed to be an x after the -24?
The reason I ask that is I don't think when you are advanced
enough to be studying circles, that your teacher would
still be testing you on such an elementary thing as to see
whether you could combine the terms -24 and -100. So I'm going
to assume you really meant:
----------------------------------------------
Are you sure there wasn't supposed to be an x after the -24?
The reason I ask that is I don't think when you are advanced
enough to be studying circles, that your teacher would
still be testing you on such an elementary thing as to see
whether you could combine the terms -24 and -100. So I'm going
to assume you really meant:
 First of all notice that every term is divisible by 4,
so let's divide every term by 4:
First of all notice that every term is divisible by 4,
so let's divide every term by 4:
 Let's group the the two terms in x first and the two terms
in y second, and add 25 to both sides:
Let's group the the two terms in x first and the two terms
in y second, and add 25 to both sides:
 To complete the square of the first two terms
To complete the square of the first two terms 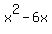 we take the coefficient of x, which is -6, multiply it by
we take the coefficient of x, which is -6, multiply it by  ,
getting -3, then we square -3, and ,
getting -3, then we square -3, and  is 9, so we add is 9, so we add 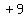 to both sides:
to both sides:
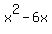   Let's put parentheses around the first three terms and
combinethe terms on the right.
Let's put parentheses around the first three terms and
combinethe terms on the right.
 Now lwt's complete the square of the last two terms
Now lwt's complete the square of the last two terms 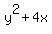 on the left side. We take the coefficient of y, which is 4,
multiply it by
on the left side. We take the coefficient of y, which is 4,
multiply it by  , getting 2, then we square 2, and , getting 2, then we square 2, and
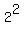 is 4, so we add is 4, so we add 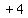 to both sides: to both sides:
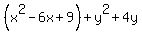   Let's put parentheses around the last three terms on the left
side and combine the terms on the right:
Let's put parentheses around the last three terms on the left
side and combine the terms on the right:
 Now factor the trinomials in the two parentheses:
Now factor the trinomials in the two parentheses:
 That can be written as
That can be written as
 In fact you could have skipped the step before that.
That's the standard form for a circle
In fact you could have skipped the step before that.
That's the standard form for a circle
 which has center (h,k) and radius r
which has center (h,k) and radius r
 is the equation for a circle which has center
(3,-2) and radius
is the equation for a circle which has center
(3,-2) and radius  which is about 6.16
and has this graph: which is about 6.16
and has this graph:
 Edwin
Edwin
|
|
|
| |