|
Question 253167: Explanation of functions. I need to make a logo that I must create from functions I know. To get a good grade I must use functions that I haven't seen before. However, I am having a hard time understanding new functions over the internet. These are the functions that I know.
-Linear (y=ax+b)
-Quadratic (Parabole)
-Absolute Value
-Exponential
-Square root
-Rational (y=a/x-h +k)
-... stairs one: y=a[b(x-h)]+k
Sorry, I study in french and I hope this is clear enough. I need at least 2 new functions explained with detail please. I am allowed to use the circle. I think that will be a simple one. I must determine a Domain(?) and a Image(?) Hope I said it right. I need to be able to find the rule (?)for the function from the graphic and how I did it. If I don't get help before tuessday january 5th then I die :( Maybe you can just point me to a good simple site that explains functions well. I apreciate any help :) Dont consider my language as a problem I can learn the terms you use fast. THANK YOU
Answer by drk(1908)   (Show Source): (Show Source):
You can put this solution on YOUR website! Joyeau anniversarie? my French is very bad . .
Let's give you a cubic function and a circle.
First the cubic function can be expressed as:

where h,k is a "locator point".
The domain of this is all reals.
The range of this is all reals.
--
Second the circle function can be expressed as:
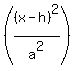 + + 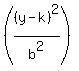 = = 
where the center is h,k and a = b.
The domain of a circle is from -h to +h and the range is from -k to +k.
--
Back to your other functions:
linear (Y = mX + b)
domain: all reals, assuming it is not vertical.
range: all reals
--
quadratic (y + aX^2 + bX + c)
if opens up,
domain: all reals
range: y >= f(-b/2a)
if opens down,
domain : all reals
range: y <= f(-b/2a)
--
absolute value (y = a/x-h/ + k)
works the same as parabola.
--
exponential (y = a*e^(x))
growth has locator point at (0,a)
domain: all reals
range: y > 0.
horizontal asymptote at y = 0
decay has locator point at (0,a)
domain: all reals
range: y > 0.
horizontal asymptote at y = 0
--
square root Y = asqrt(x-h) + k
locator point is at (h,k)
domain: x >= h
range: y >=0.
--
rational functions y = p(x) / q(x)
Domain is a bit tricky here.
question #1 - is the variable in the denominator?
If yes, the denominator not = 0 and solve for x.
If no, then
question #2 - is the variable in a square root?
If yes, then square root information >= 0and solve for x.
If no, then you have answered no two times and can say domain all reals.
range:
If the degree of the numerator is > degree of denominator, then range: all reals.
If the degree of the numerator is = degree of denominator, then range: coefficient numbers.
If the degree of the numerator is < degree of denominator, then range: can't equal 0.
I hope that helps.
|
|
|
| |