Question 253132: Determine the quadratic equation whose roots have a sum of 12 and the roots difference is 4i. (Write a let statement to identify your roots)
Found 3 solutions by richwmiller, Alan3354, MathTherapy:
Answer by richwmiller(17219)   (Show Source): (Show Source):
Answer by Alan3354(69443)   (Show Source): (Show Source):
Answer by MathTherapy(10556)   (Show Source): (Show Source):
You can put this solution on YOUR website! To find any quadratic equation of the form  , we have to realize that: , we have to realize that:
a = 1 (always)
b = - (sum of roots)
c = product of roots
Since a is always 1, and the sum of the roots = 12, then b = - (12) = -12
We now have: 
To find c, we need to 1st determine the roots and multiply them
Let root 1 be  , and root 2, , and root 2, 
Since the sum of the roots = 12, then -----  --------- eq (i) --------- eq (i)
Also, since the roots difference = 4i, then  --------- eq (ii) --------- eq (ii)
Adding equations (i) & (ii), we get: 
 or or 
Substituting 6 + 2i for  in eq (i), we get: in eq (i), we get: 


Since we now have both roots,  and and  , we multiply these two roots to get c. , we multiply these two roots to get c.
Therefore, c = (6 + 2i)(6 2i) = 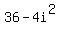 , or, 36 4(-1) = 40 , or, 36 4(-1) = 40
With a being 1, b being 12, and c being 40, the quadratic equation in the form  = = 
|
|
|