Question 253049: If x is a positive integer, which of the following CANNOT be an integer?
(A)  (B) (B) 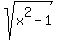 (C) (C) 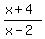 (D) (D)  (E) (E) 
Found 4 solutions by JimboP1977, comfuse, ikleyn, greenestamps:
Answer by JimboP1977(311)   (Show Source): (Show Source):
You can put this solution on YOUR website! B) because if you square a positive number you get a whole number. If you take one away from the number and reverse the process (square root) you must get a number that is not an integer.
Answer by comfuse(1)   (Show Source): (Show Source):
You can put this solution on YOUR website! The answer is D.
For  , the function evaluates to 2. Furthermore, since the function is strictly decreasing as , the function evaluates to 2. Furthermore, since the function is strictly decreasing as  increases (its derivative is negative for all increases (its derivative is negative for all  ), all positive values evaluate to strictly less than 2. Lastly, the fraction has a vertical asymptote of ), all positive values evaluate to strictly less than 2. Lastly, the fraction has a vertical asymptote of  (the ratio of the leading coefficients of numerator and denominator), which means the expression is also strictly larger than 1. (the ratio of the leading coefficients of numerator and denominator), which means the expression is also strictly larger than 1.
In conclusion, for all positive integers, the function always evaluates to strictly less than 2 and strictly larger than 1, hence, never an integer.

Answer B is not correct, as for  it evaluates to 0, which is an integer. it evaluates to 0, which is an integer.
Answer by ikleyn(52812)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Dear visitor @comfuse, the investigator of AI.
Your writing is somehow out of Math, since in your solution you write
"the fraction has a vertical asymptote of y=1 (the ratio of the leading coefficients of numerator and denominator),"
while the line y=1 is a horizontal asymptote.
Also, option (B) is a correct positive answer for x= 1, despite of your disproof.
It is typical for the AI in its current state, when it is nourished by persons,
that do not know what it is to write Math accurately.
==================
In my life, so far, I looked 4 times in the Internet for solutions to simple,
absolutely regular (= routine) mathematical problems made by AI.
I did it due to my curiosity.
All 4 solutions were incorrect.
It determines my view and my estimate of the current AI in Math education.
Pure speculation in combination with complete irresponsibility.
More harm than good.
Answer by greenestamps(13203)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Look for counterexamples for each answer choice -- that is, positive values of x for which the expression is an integer.
(A) 
x=1 yields value 0, which is an integer
(B) 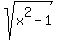
again x=1 yields value 0
(C) 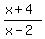
x=3 makes the denominator 1 and so yields an integer value
(E) 
x=4 yields value 1, which is an integer
(D) 
I left this for last, because (D) is the answer.
To see this, note that 
In that reformatted expression, 1 is an integer, so 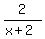 must be an integer. But must be an integer. But 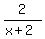 is an integer only when (x+2) is a factor of 2 -- i.e., when (x+2) is -2, -1, 1, or 2 -- and x is not a positive integer for any of those. is an integer only when (x+2) is a factor of 2 -- i.e., when (x+2) is -2, -1, 1, or 2 -- and x is not a positive integer for any of those.
ANSWER: (D)
|
|
|