Question 252882: If n < 0, which of the following could be true?
I. 2n < n^2
II. 2n < n
III. n^2 < – n
(A) None (B) I only (C) I and II only
(D) I and III only (E) I, II, and III
Found 3 solutions by edjones, drk, Edwin McCravy:
Answer by edjones(8007)   (Show Source):
Answer by drk(1908)  (Show Source):
You can put this solution on YOUR website! Here is the question:
If n < 0, which of the following could be true?
I. 2n < n^2
II. 2n < n
III. n^2 < – n
---
sometimes it is easier to plug in possible values: Let n = -1 and then check n = -1/2. This is a common SAT question and technique for solving them.
First n = -1.
(i) 2(-1) < (-1)^2 - -> TRUE
(ii) 2(-1) < (-1) - - > TRUE
(iii) (-1)^2 < -(-1) - -> FALSE
Second n = -1/2
(i) 2(-1/2) < (-1/2)^2 - -> TRUE
(ii) 2(-1/2) < (-1/2) - - > TRUE
(iii) (-1/2)^2 < -(-1/2) - -> FALSE
--
So only i and ii are true, which is choice [C]
Answer by Edwin McCravy(20060)  (Show Source):
You can put this solution on YOUR website!
I.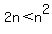 
is always true if  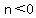, because if we divided both sides
by n, a negative number, the inequality would be reversed
and we'd have
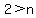and 2 is always greater than any negative number n.
II.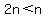 
is always true because if we divided both sides by n,
which is a negative number, the inequality would be
reversed and we'd have
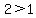and that is always true.
III.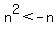 
That's true sometimnes but not always. If we divided through
by n, which is a negative number, the inequality would be
reversed and we'd have
So that would be true sometimes, like when 
but would be false, like when 
But since the word is "could be true" and not
"always true", we have to include it too,
so the answer is (E) I, II, and III
It it had says "always" instead of "could" then the
answer would have been C. But since it's "could"
it's E.
Edwin
|
|
|
