Question 252782: A road is to be constructed perpendicular to an established road. A surveyor determines that the original road passes through the points (4,9) and (2,13). The roads must intersect at (4,9) Write the equation of the second road.
Found 3 solutions by rapaljer, checkley77, JimboP1977:
Answer by rapaljer(4671)   (Show Source):
You can put this solution on YOUR website! The slope of the established road is  .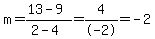
The slope of the perpendicular road is the negative reciprocal = 1/2. If it passes through the point (4,9), then you would probably want to use the point slope formula:
y-9=1/2(x-4)
y-9=1/2x-2
Add +9 to each side:
y=1/2x-2+9
y=1/2x+7
Dr. Robert J. Rapalje, Retired
Seminole State College of Florida
Answer by checkley77(12844)  (Show Source):
You can put this solution on YOUR website! I always thought perpendicular meant at right angles rather than parallel?
First road slope:
Slope=(13-9)/(2-4)=4/-2=-2
Equation for the original road:
y=-2x+9 (red line)
Parallel road slope=-2
Y=mX+b
9=-2*4+b
9=-8+b
b=9+8
b=17 is the Y intercept of the parallel road.
Equation for the pasrallel road. (green line)
 (graph 300x200 pixels, x from -6 to 10, y from -10 to 20, of TWO functions -2x +9 and -2x +17).
Answer by JimboP1977(311)  (Show Source):
|
|
|
