|
Question 252676: let f(x)=3x-6 and g(x)=x-2. find the g/f and state its domain.
Found 2 solutions by drk, Edwin McCravy:
Answer by drk(1908)   (Show Source): (Show Source):
You can put this solution on YOUR website! WE have two functions:
(i) f(x)=3x-6
(ii)g(x)=x-2
Now, F(x) / g(x) will be
(iii) 3x-6 / (x-2)
At this point we must look at domain. We have variables in the denominator. Set the denominator = 0 and solve for x.
x-2 = 0 - - > x = 2 is the restriction on the domain.
Back to the fraction . . .
We can factor the numerator as 3(x-2). We get
(iv) 3(x-2) / (x-2) = 3.
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
You can put this solution on YOUR website! Note: The other tutor mistakenly did f/g, not g/f.
Solution by Edwin:
 , ,
This function g/f is not defined when the denominator
equals 0. The denominator would equal 0 when  which simplifies to when
which simplifies to when  . Therefore
x cannot equal 2, and 2 cannot be part of the domain
of g/f. However when . Therefore
x cannot equal 2, and 2 cannot be part of the domain
of g/f. However when  , the right side , the right side
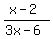 can be simplified to can be simplified to
 However that cancellation cannot be made when
However that cancellation cannot be made when  !,
since the function is undefined there, but it can be done
for every other value of x.
So therefore we can express g/f in its simplest form
this way: !,
since the function is undefined there, but it can be done
for every other value of x.
So therefore we can express g/f in its simplest form
this way:
 , ,  Its graph is the green graph below. It is the horizontal
green line with a hole in it where the point (2,
Its graph is the green graph below. It is the horizontal
green line with a hole in it where the point (2, )
is missing and that point is NOT part of the graph of g/f: )
is missing and that point is NOT part of the graph of g/f:
 So the domain of g/f is the x-axis without a value at 2.
In set-builder notation the domain of g/f would be
written
So the domain of g/f is the x-axis without a value at 2.
In set-builder notation the domain of g/f would be
written 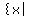   .
The graph of its domain on a number line would look just
like the x-axis above only, shaded everywhere except at 2,
and with an open circle at 2, like this:
<========================o========>
-4 -3 -2 -1 0 1 2 3 4
In interval notation this domain is written .
The graph of its domain on a number line would look just
like the x-axis above only, shaded everywhere except at 2,
and with an open circle at 2, like this:
<========================o========>
-4 -3 -2 -1 0 1 2 3 4
In interval notation this domain is written
    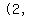   Edwin
Edwin
|
|
|
| |