Question 252614: Can you help me solve this questions, please?
The original ferris wheel, designed by George Ferris, was 250 feet in diameter. Making 1 revolution for every 40 seconds, h(t)=125sin(0.157t -pi/2) +125 represents the height h (feet) of a seat on the wheel at any time t (seconds). The ride begins when t = 0. During the first 30 seconds of the ride, at what time is a rider on the ferris wheel exactly 125 feet above the ground?
and also, help me with:
approximate the solution to 2cosx+x=0 to the nearest hundredth.
Hints: it should be in radian mode and there are no () around the x+x
Thanks so much!!
Found 2 solutions by jim_thompson5910, drk:
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website!  Start with the given equation. Start with the given equation.
 Plug in Plug in 
 Subtract 125 from both sides. Subtract 125 from both sides.
 Combine like terms. Combine like terms.
 Divide both sides by 125. Divide both sides by 125.
 Reduce. Reduce.
 Rearrange the equation Rearrange the equation
 Take the arcsine of both sides. Take the arcsine of both sides.
 or or  Evaluate the arcsine of 0 to get Evaluate the arcsine of 0 to get  or or  . Don't forget to add in integer multiples of . Don't forget to add in integer multiples of 
---------------------------Side Note----------------------
Take note how if  , then we just get 0 or , then we just get 0 or  . If . If  , then we get , then we get  or or  . If we continue this, we can see that we'll hit all of the integer multiples of . If we continue this, we can see that we'll hit all of the integer multiples of  . Because of this we can condense the right side to just . Because of this we can condense the right side to just 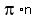 . .
--------------------------------------------------------
 Condense the right side (see side note above). Condense the right side (see side note above).
 Add Add  to both sides. to both sides.
 Combine like terms. Combine like terms.
 Multiply both sides by Multiply both sides by 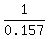 to isolate 't'. to isolate 't'.
 Multiply. Multiply.
Now let's plug in some values of 'n'. If n=0, then 
If n=1, then  . However, since we're only worried about the first 30 seconds, this means that . However, since we're only worried about the first 30 seconds, this means that  which would exclude the 't' value when which would exclude the 't' value when  . Any other value of 'n' will generate a 't' value outside the interval . Any other value of 'n' will generate a 't' value outside the interval 
=====================================
Answer:
So the only solution is  (which is approximate) which means that at about 10.00507 seconds, the rider will be 125 feet above the ground during the first 30 seconds. (which is approximate) which means that at about 10.00507 seconds, the rider will be 125 feet above the ground during the first 30 seconds.
===========================================================================
# 2
Since the variable we want to solve for in  is buried in a trig function and is outside the trig function, there is no way to solve for it exactly. is buried in a trig function and is outside the trig function, there is no way to solve for it exactly.
So we have to use a graphing calculator to approximate the roots of 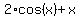 . Graphing the given expression, we get . Graphing the given expression, we get

Graph of 
Now use the graphing calculator's root/zero function to find the approximate root of  which rounds to which rounds to  to the nearest hundredth. to the nearest hundredth.
So the answer is 
Answer by drk(1908)   (Show Source): (Show Source):
You can put this solution on YOUR website! QUESTION #1: We have the formula

we want the h(t) = 125. So,
125 =125sin(0.157t -pi/2) + 125
0 = sin(0.157t -pi/2)
sin^-1(0) = (0.157t -pi/2)
{0, PI} = (0.157t -pi/2)
At this point we split and solve:
0 = (0.157t -pi/2)
pi/2 = .157t
*
t = 10 seconds
pi = (0.157t -pi/2)
3pi/2 = .157t
t = 30 seconds.
----
QUESTION #2: approximate the solution to 2cosx+x=0 to the nearest hundredth.
2cosx + x = 0
2cosx = -x
cosx = -(1/2)x
I don't see any solutions.
|
|
|