SOLUTION: The height of the ocean at the dock is modeled by the function, h= 3sin(pi*t/4) +5 where h is measured in feet and t is the time in hours. If t=0 refers to 12:00 a.m., what is the

Algebra ->  Trigonometry-basics -> SOLUTION: The height of the ocean at the dock is modeled by the function, h= 3sin(pi*t/4) +5 where h is measured in feet and t is the time in hours. If t=0 refers to 12:00 a.m., what is the       Log On


   

Question 252605: The height of the ocean at the dock is modeled by the function, h= 3sin(pi*t/4) +5 where h is measured in feet and t is the time in hours. If t=0 refers to 12:00 a.m., what is the height of the ocean at 10:00 a.m.?
find the exact value of the vertical asymptotes for 0<=x<=pi for the function y=cot(3x)
if sin(x)= -3/5 with x in the quadrant 4, find the sec(x)
Thanks so much!!
Answer by jim_thompson5910(35256) About Me  (Show Source):
You can put this solution on YOUR website!
I'll do the first two to get you going.

# 1

Since "t=0 refers to 12:00 a.m", this means that t=10 refers to 10:00 a.m. (just add 10 hours to 0)


h=3%2Asin%28pi%2At%2F4%29%2B5 Start with the given equation.


h=3%2Asin%28pi%2A10%2F4%29%2B5 Plug in t=10


h=3%2Asin%28pi%2A5%2F2%29%2B5 Reduce.


h=3%2Asin%285pi%2F2%29%2B5 Rearrange the terms


h=3%2Asin%285pi%2F2-2pi%29%2B5 Subtract 2pi from the argument (this is valid because you'll end up on a coterminal angle).


h=3%2Asin%28pi%2F2%29%2B5 Combine like terms.


h=3%2A1%2B5 Use the unit circle to evaluate the sine of pi%2F2 to get 1.


h=3%2B5 Multiply


h=8 Add


So the height of the ocean at 10:00 a.m. is 8 feet.


=================================================================

# 2

Remember that cot%28x%29=1%2Ftan%28x%29 and tan%28x%29=sin%28x%29%2Fcos%28x%29. So this means that cot%283x%29=1%2Ftan%283x%29=1%2F%28sin%283x%29%2Fcos%283x%29%29=cos%283x%29%2Fsin%283x%29 or in short, cot%283x%29=cos%283x%29%2Fsin%283x%29


To find the vertical asymptotes of cot%283x%29=cos%283x%29%2Fsin%283x%29, we'll set the denominator equal to zero and solve for 'x' (since division by zero is undefined).


sin%283x%29=0 Set the denominator equal to zero.


3x=arcsin%280%29 Take the arcsine of both sides.


x=0%2B2pi%2An or x=pi%2B2pi%2An Evaluate the arcsine of 0 to get x=0 or x=pi. Don't forget to add on multiples of 2pi to each solution.


x=%280%2B2pi%2An%29%2F3 or x=%28pi%2B2pi%2An%29%2F3 Divide both sides by 3 to isolate 'x' in each case.

As a shortcut, you can condense the solution to x=%281%2F3%29pi%2An where 'n' is an integer.


So if x=%281%2F3%29pi%2An, where 'n' is an integer, then sin%283x%29=0.


But since 0%3C=x%3C=pi, this means that we're only going to look at the solutions x=0 (for n=0), x=pi%2F3 (where n=1), x=2pi%2F3 (when n=2), and x=pi (when x=3). Note: any other solution is outside the interval 0%3C=x%3C=pi.


So the four vertical asymptotes of 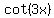cot%283x%29 are x=0, x=pi%2F3, x=2pi%2F3, and x=pi