I'm really bad at word problems. This one i am lost and i don't get.
Find 3 consecutive even numbers
That's 
, the smallest, 
, the middle sized,
and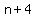 
, the largest
where the product of the smaller two numbers
That product is times , which is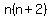 
is 64 less than of the square of the largest number.
That means that that product is equal to the largest number, ,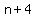
squared or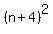 
, with 
subtracted from it. That is,
that product is equal to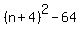 
So it's nothing but the equation:
See? It just takes reading carefully and thinking about what
it really says about those unknown even integers. Can you now solve
that equation? If not post again asking how. The answer is
, so the three consectutive even integers are 
,
,
and 
.
And you can easily check it:
the product of the smaller two numbers is 8x10 or 80,
and 80 really is 64 less than 144, which the largest,
12, squared.
Edwin
