|
Question 252191: A two digit number has different digits. If the difference between the square of the number and the square of the number whose digits are interchanged is a positive perfect square, what is the two digit number?
Found 2 solutions by drk, Edwin McCravy:
Answer by drk(1908)   (Show Source): (Show Source):
Answer by Edwin McCravy(20055)   (Show Source): (Show Source):
You can put this solution on YOUR website!
This time drk's solution was shorter than mine. Essentially he
took square roots of both sides of
 getting
getting
 Ssince the right side is a positive integer, the left side must
be also. That means there must be another factor of 11 under
the square root radical, and the only possibility of the sum of
two digits being a multiple of 11 is for (t+u) to be 11, and that
is only true when t=6 and t=5.
Here was my longer solution:
-----------------------------
Ssince the right side is a positive integer, the left side must
be also. That means there must be another factor of 11 under
the square root radical, and the only possibility of the sum of
two digits being a multiple of 11 is for (t+u) to be 11, and that
is only true when t=6 and t=5.
Here was my longer solution:
-----------------------------
A two digit number has different digits. If the difference between the square of the number and the square of the number whose digits are interchanged is a positive perfect square, what is the two digit number?
There must exist integer k so that:
 Factor the left side as the difference of two perfect squares:
Factor the left side as the difference of two perfect squares:
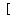 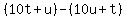 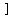 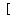 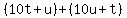 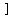   Simplifying:
Simplifying:
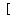 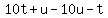 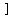 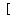  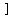  



 Write 99 as a product of primes:
Write 99 as a product of primes:
 Since the left side is an integer, the right side must be also.
So
Since the left side is an integer, the right side must be also.
So  must contain factors must contain factors 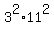 as well as
possibly another perfect square as well as
possibly another perfect square 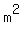 .
So .
So  must be a perfect square of the form must be a perfect square of the form 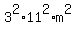 ,
where m is a positive integer. ,
where m is a positive integer.
 That gives:
That gives:
 The largest possible value of (t-u)(t+u) is
when t=9 and u=0, or (9-0)(9+0)=81 and the smallest
is when t=1 and u=0, or (1-0)(1+0)=1. Therefore the
right side must satisfy this:
The largest possible value of (t-u)(t+u) is
when t=9 and u=0, or (9-0)(9+0)=81 and the smallest
is when t=1 and u=0, or (1-0)(1+0)=1. Therefore the
right side must satisfy this:


 since 4 is the largest perfect
square that does not exceed since 4 is the largest perfect
square that does not exceed 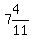 , and since
1 is the smallest largest perfect square that exceeds , and since
1 is the smallest largest perfect square that exceeds
 .
Therefore .
Therefore
 So m is either 1 or 2.
When m = 2, we have
So m is either 1 or 2.
When m = 2, we have
 The only ways 44 can be written as the product of two
integers are 1*44, 2*22, and 4*11. But the larger factor,
t+u cannot be more than 9+8 or 17, thus that would leave
only 4*11. 4 is even and 11 is odd. However t-u and t+u
are either both even or both odd. So we have ruled out
m = 2.
That leaves only the possibility
m = 1 and
The only ways 44 can be written as the product of two
integers are 1*44, 2*22, and 4*11. But the larger factor,
t+u cannot be more than 9+8 or 17, thus that would leave
only 4*11. 4 is even and 11 is odd. However t-u and t+u
are either both even or both odd. So we have ruled out
m = 2.
That leaves only the possibility
m = 1 and
 Since 11 is prime, the only two positive integer factors it has
are 1 and 11. Therefore the smaller factor
Since 11 is prime, the only two positive integer factors it has
are 1 and 11. Therefore the smaller factor 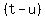 must be 1
and the larger factor 11. So we have the system of equations: must be 1
and the larger factor 11. So we have the system of equations:
 Solving that gives us t=6 and u=5, which both can be digits.
So the only solution is the two digit number 65.
Edwin
Solving that gives us t=6 and u=5, which both can be digits.
So the only solution is the two digit number 65.
Edwin
|
|
|
| |