SOLUTION: A box contains 2 green and 3 white balls. A ball is selected at random from the box. If the ball is green, a card is drawn from a deck of 52 ca rdto. If the ball is white, a card i

Algebra ->  Probability-and-statistics -> SOLUTION: A box contains 2 green and 3 white balls. A ball is selected at random from the box. If the ball is green, a card is drawn from a deck of 52 ca rdto. If the ball is white, a card i      Log On


   

Question 252130: A box contains 2 green and 3 white balls. A ball is selected at random from the box. If the ball is green, a card is drawn from a deck of 52 ca rdto. If the ball is white, a card is drawn from the deck consisting of just the 16 pictures. (a) What is the probability of drawing a. king? (b) What is the probability of a white ball was selected given that a king was drawn?
Answer by Edwin McCravy(20060) About Me  (Show Source):
You can put this solution on YOUR website!
A box contains 2 green and 3 white balls. A ball is selected at random from the box. If the ball is green, a card is drawn from a deck of 52 ca rdto. If the ball is white, a card is drawn from the deck consisting of just the 16 pictures. 

I don't get the "deck consisting of just the 16 pictures" since there are
only 12 picture cards (Jack, Queen and King of the 4 suits) in a standard deck
of 52. Perhaps this problem considers Aces to be picture cards. But I will
assume there are 16 picture cards anyway)

(a) What is the probability of drawing a king? 

P(green)=%22P%28G%29%22=2%2F5
P(white)=%22P%28W%29%22=3%2F5
P(king from deck of 52)=4%2F52=1%2F13
P(king from 16 picture-card deck)=4%2F16=1%2F4
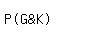P(green and king) = %22P%28G%26K%29%22=%282%2F5%29%281%2F13%29=2%2F65
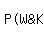P(white and king) = %22P%28W%26K%29%22=%283%2F5%29%281%2F4%29=3%2F20
P(king) = P(G&K OR W&K) = 2%2F65%2B3%2F20=47%2F260
= 2%2F65%2B3%2F20=47%2F260, about 18% of the time.

(b) What is the probability of a white ball was selected given that a king was drawn?




or about 83% of the time.



Edwin