Question 251829: x^2+2x+9
I have tried x={-2ħsqrt(2^2-4*1*9)}/2*1
(quadratic formula: x={-bħsqrt( b^2-4ac)}/2(a))
Process:
x={-2ħsqrt(2^2-4*1*9)}/2(1)
x={-2ħsqrt(4-36)}/2
x=(-2/2)ħ{sqrt-32/2}
x=-1ħ(sqrt-32/2)
Looking for -1ħ2i*sqrt(2), but I can't get there.
I need the process to find this imaginary root.
what am I doing wrong?
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! The trick here lies in simplifying 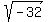
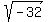 Start with the given expression Start with the given expression
 Factor out a negative 1 Factor out a negative 1
 Break up the square roots using the identity Break up the square roots using the identity 
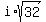 Replace Replace 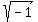 with with  (remember (remember  ) )
Now lets simplify  : :
The goal of simplifying expressions with square roots is to factor the radicand into a product of two numbers. One of these two numbers must be a perfect square. When you take the square root of this perfect square, you will get a rational number.
So let's list the factors of 32
Factors:
1, 2, 4, 8, 16, 32
Notice how 16 is the largest perfect square, so lets factor 32 into 16*2
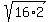 Factor 32 into 16*2 Factor 32 into 16*2
 Break up the square roots using the identity Break up the square roots using the identity 
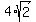 Take the square root of the perfect square 16 to get 4 Take the square root of the perfect square 16 to get 4
This means that the expression  simplifies to simplifies to 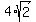
So the expression 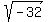 simplifies to simplifies to 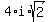 (just reintroduce (just reintroduce  back in) back in)
In other words, 
----------------------------------------------------------------------
Going back to  , this expression simplifies to , this expression simplifies to  . From there, it reduces to . From there, it reduces to 
So the solutions are  or or 
|
|
|