Question 251578: Can someone help me with these two questions? Thanks
1. Evaluate the exponential equation for three positive values of x, three negative values of x, and at x=0. Transform the second expression into the equivalent logarithmic equation; and evaluate the logarithmic equation for three values of x that are greater than 1, three values of x that are between 0 and 1, and at x=1. Use the resulting ordered pairs to plot the graph of each function; y=2^x, x=2^y
8. Evaluate the exponential function for three positive values of x, three negative values of x, and at x=0. Show your work. Use the resulting ordered pairs to plot the graph; State the domain and the range of the function.
f(x) = e^-x -1
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! first equatioon is y = 2^x
values of x are:
-3
-2
-1
0
1
2
3
when x = -3, 2^x = 2^(-3) = 1/2^3 = 1/8
when x = -2, 2^x = 2^(-2) = 1/2^2 = 1/4
when x = -1, 2^x = 2^(-1) = 1/2^1 = 1/2
when x = 0, 2^x = 2^0 = 1
when x = 1, 2^x = 2^1 = 2
when x = 2, 2^x = 2^2 = 4
when x = 3, 2^x = 2^3 = 8
graph of the equation looks like this:
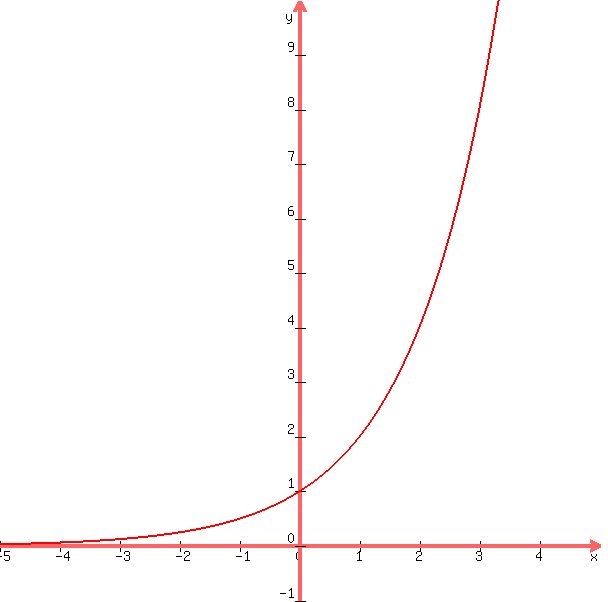
---------------------------------------------------------------------------
x = 2^y if and only if 
this is the same as 
values for x are:
.1
.4
.7
1
2
3
4
when x = .1, y = 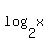 = =  = = 
when x = .4, y = 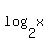 = = 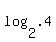 = = 
when x = .7, y = 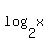 = = 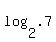 = = 
when x = 1, y = 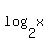 = =  = = 
when x = 2, y = 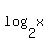 = =  = = 
when x = 3, y = 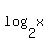 = = 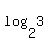 = = 
when x = 4, y = 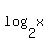 = = 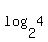 = = 
graph of this equation looks like this:
----------------------------------------------------------------------------
graph of both equations together looks like this:

since the equation of y = 2^x is the inverse of equation x = 2^y, these equations are symmetric about the line y = x as shown in the graph.
-------------------------------------------------------------------------------
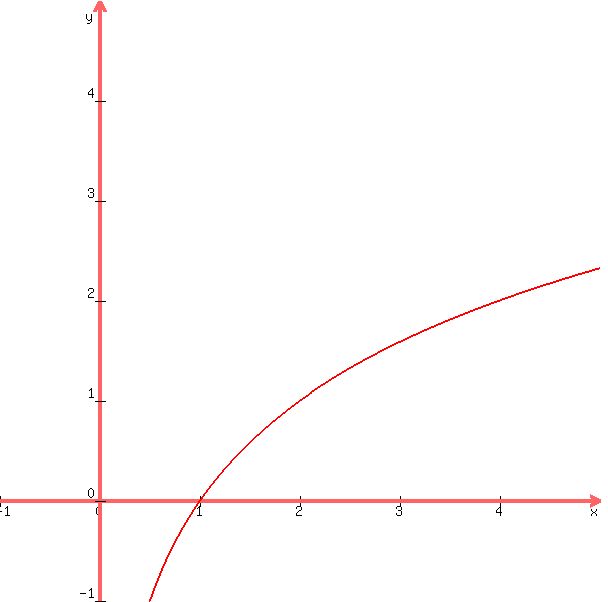
8. Evaluate the exponential function for three positive values of x, three negative values of x, and at x=0. Show your work. Use the resulting ordered pairs to plot the graph; State the domain and the range of the function.
f(x) = e^-x -1
equation is 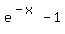
values of x are:
-3,-2,-1,0,1,2,3
when x = -3, equation becomes 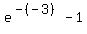 = =  = 19.08553692 = 19.08553692
when x = -2, equation becomes 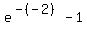 = = 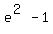 = 6.389056099 = 6.389056099
when x = -1, equation becomes 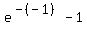 = =  = 1.718281828 = 1.718281828
when x = 0, equation becomes  = 0 = 0
when x = 1, equation becomes 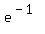 = -.632120559 = -.632120559
when x = 2, equation becomes  = -.864664717 = -.864664717
when x = 3, equation becomes  = -.950212932 = -.950212932
graph of equation looks like this:

the domain of the equation is all real values of x.
the range of the equation is all real values of y > -1
x will never be less then or equal to -1.
|
|
|