Question 251273: for the following problems, determine how many years it will take for the two accounts the reach the same amount.
a $1000 investment at a rate of 3% compounded monthly and an $1100 investment at a rate of 3.02% compounded annually.
a $2000 investment at a rate of 4%compounded continuously and a $3000 investment at a rate of 5% compounded monthly
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! formula is:
f = p * (1+i)^n
f = future amount
p = present amount
i = interest rate per time period
n = number of time periods
interest rate = interest rate percent divided by 100 percent.
example:
3% / 100% = .03 which is the interest rate. 3% was the interest rate percent.
you have to adjust your annual interest rate to an interest rate per time period.
annual interest rate is interest rate per year.
if your time period is in years, no adjustment needs to be made.
if your time period is in months, then the annual interest rate needs to be divided by 12 to become a monthly interest rate.
your number of time periods have to be adjusted if they are not in the same denomination.
if your number of time periods are in years, then your number of years does not need to be adjusted.
if your number of time periods is in months, then your number of years needs to be multiplied by 12 in order to be in months.
------------------------------------------------------------------------------
PROBLEM NUMBER 1
a $1000 investment at a rate of 3% compounded monthly and an $1100 investment at a rate of 3.02% compounded annually.
$1000 at 3% compounded monthly formula would be:
f = p*(1+i)^n
p = 1000
i = 3% / 100% / 12 = .0025
y = number of years
n = y*12
formula becomes:
f = 1000*(1.0025)^(12*y)
$1100 at 3.02% compounded annually formula would be:
p = 1100
i = 3.02% / 100% = .0302
y = number of years
n = y
formula becomes:
f = 1100*(1.0302)^(y)
for the investments to be equal, f[1] = f[2] making the equations equal to each other.
you get:
1000*(1.0025)^(12*y) = 1100*(1.0302)^(y)
you need to solve for y.
divide both sides of this equation by (1.0302)^(y) and divide both sides of this equation by 1000 to get:
(1.0025)^(12*y) / (1.0302)^(y) = 1100/1000
take the log of both sides of this equation to get:

since log(a/b) = log(a) - log(b), this equation becomes:

since log(a^b) = b*log(a), this equation becomes:

factor out the y to get:

divide both sides of this equation by  to get: to get:

solve for y to get:
y = 454.7149479 years.
the investments will break even in 454.7149479 years.
to confirm this answer is correct, substitute in the original equations.
f = 1000*(1.0025)^(12*y) results in f = 826061905.3
f = f = 1100*(1.0302)^(y) results in f = 826061905.3
they are the same which satisfies the problem statement.
if you take any number of years less than 454, the monthly equation will yield less. if you take any number of years greater than 455, the monthly equation will yield more.
------------------------------------------------------------------------------
PROBLEM NUMBER 2
the continuous compounding formula is different.
that formula would be:

f = future value
p = present amount
r = annual interest rate
y = number of years
you have two formulas that will be compare with each other to provide the solution to this problem.
they are the continuous compounding formula just described, and

f = future value
p = present amount
r = annual interest rate
c = number of compounding periods per year
y = number of years
your problem statement is:
a $2000 investment at a rate of 4% compounded continuously and a $3000 investment at a rate of 5% compounded monthly
with an investment of 2000 at 4% compounded continuously, the formula of:
 becomes: becomes:

with an investment of 3000 at 5% compounded monthly, the formula of:
 becomes: becomes:
 which becomes: which becomes:

the investments are equal when the 2 equations are equal to each other.
you get:

divide both sides of this equation by 3000 and divide both sides of this equation by 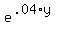 to get: to get:

take the log of both sides of this equation to get:

since  , your equation becomes: , your equation becomes:

since  , your equation becomes: , your equation becomes:

factor out the y to get:

divide both sides of the equation by  to get: to get:

solve for y to get:
y = -40.97212172 ?????
I did not expect a negative number of years so I graphed the 2 equations to see what was going on.
The following graph shows that these 2 equations do indeed equal each other when the number of years is negative.
The graphs do not intersect at any positive value of the number of years which means the two equations will never be equivalent.
See below the graph for additional comments.
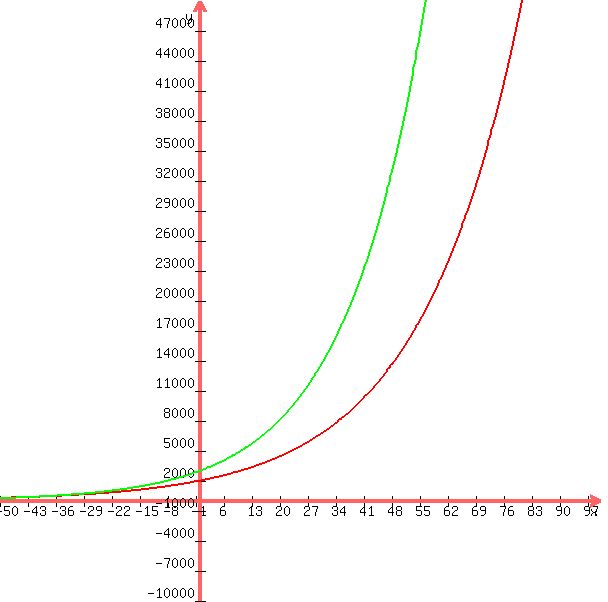
A calculation when the number of years is equal to -40.97212172 shows that the investments are equal at the value of 388.3929522.
The calculations are correct even if they were confusing.
An analysis of the continuous compounding interest rate of .04 compared to the monthly compounding interest rate of (.05/12) yields the following:
We can convert the monthly compounding rate to the equivalent continuous compounding rate to compare them directly.
The formula to create the equivalent continuous compounding rate from the monthly compounding rate is as follows:
The general process is as follows:
THE PROCESS OF CONVERTING FROM DISCRETE COMPOUNDING TO CONTINUOUS COMPOUNDING IN A NUTSHELL
You are given the nominal rate using discrete compounding.
You solve for the effective rate using discrete compounding.
You use the effective rate using discrete compounding to solve for the nominal rate using continuous compounding.
The actual process given the monthly compounding rate is as follows:
5% = .05 annual interest rate.
.05/12 = .004166667 monthly interst rate.
1.004166667^12 = Effective annual rate using monthly compounding = 1.051161898
Use this effective rate to solve for the continuous compounding rate.
The formula is:
R[e] = e^r which becomes:
1.051161898 = e^r
Take natural log of both sides to get:
ln(1.051161898 = ln(e^r)
since ln(e^r) = r*ln(e) = r*1, this equation becomes:
ln(1.051161898 = r which becomes:
r = .049896122
what this means is that compounding 5% a year monthly is equivalent to continuous compounding at 4.9896122% a year.
For example, consider an investment of 1 at 5% a years with monthly compounding for 5 years and compare it to an investment of 1 at 4.9896122% a year with continuous compounding.
1 * (1.004166667)^(5*12) = 1.283358679
1 * e^(.049896122*5) = 1.283358679
They are equivalent.
The bottom line is:
3000 at 5% a year with monthly compounding equals an equivalent continuous compounding rate of 4.98...% a year.
2000 at a continuous compounding rate of 4% a year will never catch up to it.
|
|
|