SOLUTION: The sum of two numbers is six. The sum of the squares of the two numbers is twenty. Find the two numbers. The sum of the squares of two consecutive positive integers is forty-on

Algebra ->  Customizable Word Problem Solvers  -> Numbers -> SOLUTION: The sum of two numbers is six. The sum of the squares of the two numbers is twenty. Find the two numbers. The sum of the squares of two consecutive positive integers is forty-on      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 250912: The sum of two numbers is six. The sum of the squares of the two numbers is twenty. Find the two numbers.
The sum of the squares of two consecutive positive integers is forty-one. Find the two integers.
The sum of the two numbers is ten. The product of the two numbers is twenty-one. Find the two numbers.
How many consecutive natural numbers beginning with 1 will give a sum of 78?
Answer by PRMath(133) About Me  (Show Source):
You can put this solution on YOUR website!
You asked four questions. I'll give you two answers and then you can see if it helps you. If not, re submit your other two questions.

The sum of two numbers is six. The sum of the squares of the two numbers is twenty. Find the two numbers.

Let's break down your problem and write equations. Here goes:

The sum of two numbers is six: Our equation, then, is X + Y = 6
The sum of the squares of the two numbers is twenty: Our equation, then, is x%5E2+%2B+y%5E2+=+20


So now we have a system:

X + Y = 6
x%5E2+%2B+y%5E2+=+20

Can we rewrite X + Y = 6 so that we can use the info? How about if we solve for Y? Let's do that:

X + Y = 6
Y = 6 - X

Now we can substitute the above into the 2nd equation, like this:

x%5E2+%2B+y%5E2+=+20 (2nd equation)
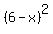x%5E2+%2B+%286+-+x%29%5E2+=+20 (See where we put in (6 - x) where the Y variable was?
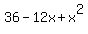
x%5E2+%2B+36+-+12x+%2B+x%5E2+=+20 The %286+-+x%29%5E2 became: (6 - x)(6 - x), which resulted in: 36+-+12x+%2B+x%5E2
2x%5E2+-+12X+%2B+16+=+0 (Combined the like terms of x%5E2+%2B+x%5E2+=+2x%5E2. Also, subtracted 20 from both sides of the equation)
2%28x%5E2+-+6x+%2B8%29+=+0 (factored out 2 from the entire equation)
x%5E2+-+6x+%2B+8+=+0 (divided 2 from both sides of the equation)
%28x+-+4%29%28x+-+2%29+=+0 (factored using FOIL)
x = 4 x = 2

Check: 4 + 2 = 6 YES
4%5E2+%2B+2%5E2+=+20
16+%2B+4+=+20 YES! :-)

Therefore, this answer checks out. :-)

Now let's try another.......


The sum of the two numbers is ten. The product of the two numbers is twenty-one. Find the two numbers.

Again, let's break down the question:

The sum of the two numbers is ten: Our equation: X + Y = 10
The product of the two numbers is twenty-one. Our equation: XY = 21

Here's another system:

X + Y = 10
XY = 21

Let's rewrite the first equation by solving for X:

X + Y = 10
X = 10 - Y

Now let's put our "X" information into the 2nd equation:

XY = 21
%2810+-+y%29y+=+21 (see where we substituted 10 - y where the X variable was?
10Y+-+y%5E2+=+21 (Distributed the "y" to 10 and then to -y)
0+=+y%5E2+-10y+%2B+21 (subtracted 10y from both sides and added y%5E2 to both sides
0+=+%28y+-+3%29%28y+-+7%29 (factored by using FOIL)
y = 3 y = 7

Let's check:
3 + 7 = 10 YES
3 x 7 = 21 YES

See if these examples help you with your other two problems. I hope they do. :-)