A. on the graph at the right solve the following system of inequalities.
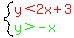 First we form the equations of the boundary lines for the problem.
The boundary lines' equations are the same as the inequalities
with the signs of inequality replaced by equal signs:
We graph this system of equations of lines:
First we form the equations of the boundary lines for the problem.
The boundary lines' equations are the same as the inequalities
with the signs of inequality replaced by equal signs:
We graph this system of equations of lines:
 by getting a couple of points on each one. But we
draw the lines dotted, not solid because the inequalities
are
by getting a couple of points on each one. But we
draw the lines dotted, not solid because the inequalities
are  , not
, not  .
.
 Now you must shade one of the four wedge shapes formed by the two
lines. The green inequality is solved for y and it's
Now you must shade one of the four wedge shapes formed by the two
lines. The green inequality is solved for y and it's 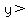 and "greater than" means "ABOVE". The red inequality is solved for
y and it's
and "greater than" means "ABOVE". The red inequality is solved for
y and it's 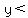 , and "less than" means "BELOW". So you
shade the wedge that is ABOVE the GREEN line and BELOW the RED line.
That's the RIGHT wedge with the * in it. This software doesn't permit
me to shade on here, but you can shade the right-most wedge on your
paper.
, and "less than" means "BELOW". So you
shade the wedge that is ABOVE the GREEN line and BELOW the RED line.
That's the RIGHT wedge with the * in it. This software doesn't permit
me to shade on here, but you can shade the right-most wedge on your
paper.
B. check your answer by substituting back into the original equations.i need help!!!!!
I'm not sure what that means. You didn't have original EQUATIONS, you
had original INEQUALITIES. Maybe that means to choose a point in the
shaded region and check it in the original inequalities to see if it
satisfies them. So lets pick a point is that wedge-shaped region on
the right, say (5,2). I have marked that point * on the graph. Substitute
it into
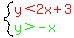
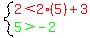 or
or
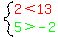 They're both true, so maybe that's what it means by those checking
instructions.
Edwin
They're both true, so maybe that's what it means by those checking
instructions.
Edwin