SOLUTION: Hi I need to solve this equation. but need help. 5^(x)=4^(x+1)[(4/5)^(x)] Thank you for your time.

Algebra ->  Logarithm Solvers, Trainers and Word Problems -> SOLUTION: Hi I need to solve this equation. but need help. 5^(x)=4^(x+1)[(4/5)^(x)] Thank you for your time.      Log On


   

Question 250502: Hi I need to solve this equation. but need help.
5^(x)=4^(x+1)[(4/5)^(x)]
Thank you for your time.
Found 2 solutions by MRperkins, jsmallt9:
Answer by MRperkins(300) About Me  (Show Source):
You can put this solution on YOUR website!
I have worked through this problem and got x=3.1064 after checking the answer, I get 148.3435=148.3369 I believe that this is close enough to say that the variance is due to rounding. If you need a fractional answer, then we can stop before computing the logarithms.
I can email you my work as an answer without work is fairly useless. I would rather help you via online whiteboard to get the answer by yourself. Email me at justin.sheppard.tech@hotmail.com and I will set up a time to help you.
Respectfully,
Justin

Answer by jsmallt9(3758) About Me  (Show Source):
You can put this solution on YOUR website!
5%5Ex=4%5E%28x%2B1%29%28%284%2F5%29%5Ex%29
First let's condense the expressions by gathering the powers of 5 and powers of 4 together. Using the property of exponents, %28a%2Fb%29%5Eq+=+a%5Eq%2Fb%5Eq we get:
5%5Ex=4%5E%28x%2B1%29%284%5Ex%2F5%5Ex%29
Multiplying both sides by 5%5Ex:
5%5Ex%2A5%5Ex=4%5E%28x%2B1%29%284%5Ex%29
Next we use the rule for exponents, a%5Ep%2Aa%5Eq+=+a%5E%28p%2Bq%29, to combine the powers of 5 and the powers of 4:
5%5E%28x%2Bx%29=4%5E%28%28x%2B1%29%2Bx%29
5%5E%282x%29+=+4%5E%282x+%2B+1%29
Our equation is now much simpler which makes it easier to solve. With the variable in the exponent, we will use logarithms to solve. Any base of logarithms can be used. But we we want to be able to find a decimal approximation of our answer, then we should pick a base that our calculator can find. I'll use base 10 since that is probably the most commonly available logarithm on calculators:
log%28%285%5E%282x%29%29%29+=+log%28%284%5E%282x+%2B+1%29%29%29
Next we use a property of logarithms, log%28a%2C+%28p%5Eq%29%29+=+q%2Alog%28a%2C+%28p%29%29, to move the exponent in the argument out in front. (This is why we use logarithms on problems like this: to get variables out of exponents,)
2x%2Alog%28%285%29%29+=+%282x%2B1%29log%28%284%29%29
With x out of the exponents we can now use "regular" Algebra to solve for it. Start by simplifying:
2x%2Alog%28%285%29%29+=+2x%2Alog%28%284%29%29+%2B+log%28%284%29%29
Gather the x terms on one side by subtracting 2x%2Alog%28%284%29%29 from each side:
2x%2Alog%28%285%29%29+-+2x%2Alog%28%284%29%29+=+log%28%284%29%29
Factor out x on the left:
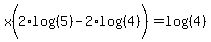
x%282%2Alog%28%285%29%29+-+2%2Alog%28%284%29%29%29+=+log%28%284%29%29
Divide both sides by %282%2Alog%28%285%29%29+-+2%2Alog%28%284%29%29%29
x+=+log%28%284%29%29%2F%282%2Alog%28%285%29%29+-+2%2Alog%28%284%29%29%29
If we want, we can simplify 2%2Alog%28%285%29%29 and , in the other direction:
x+=+log%28%284%29%29%2F%28log%28%285%5E2%29%29+-+log%28%284%5E2%29%29%29
x+=+log%28%284%29%29%2F%28log%28%2825%29%29+-+log%28%2816%29%29%29
This is an exact expression for the answer. If you want a decimal approximation, then you can use your calculator to find these 3 logarithms and then do the subtraction and division. I'll leave that up to you.

If you were never interested in decimal approximations it would have been better to use base 4 or base 5 logarithms:
  • With base 4 logarithms you would get:
    x+=+log%284%2C+%284%29%29%2F%282%2Alog%284%2C+%285%29%29+-+2%2Alog%284%2C+%284%29%29%29
    And since log%284%2C+%284%29%29+=+1 by definition we get:
    x+=+1%2F%282%2Alog%284%2C+%285%29%29+-+2%29 which is much simpler than the base 10 expression.
  • With base 5 logarithms you would get:
    x+=+log%285%2C+%284%29%29%2F%282%2Alog%285%2C+%285%29%29+-+2%2Alog%285%2C+%284%29%29%29
    And since log%285%2C+%285%29%29+=+1 by definition we get:
    x+=+log%285%2C+%284%29%29%2F%282+-+2%2Alog%285%2C+%284%29%29%29 which is also simpler than the base 10 expression (but not quite as simple as the base 4 expression).