SOLUTION: Would someone be so kind as to assist me with this problem? A football field is about 50 yards wide by 120 yards long. The border of uniform width around the entire field has an ar

Algebra ->  Customizable Word Problem Solvers  -> Misc -> SOLUTION: Would someone be so kind as to assist me with this problem? A football field is about 50 yards wide by 120 yards long. The border of uniform width around the entire field has an ar      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 249526: Would someone be so kind as to assist me with this problem? A football field is about 50 yards wide by 120 yards long. The border of uniform width around the entire field has an area of about 1800 square yards. How wide is the border around the field?
This is how I have attempted to solve the problem:
(120-2x)(50-2x)=6000-1800 length x width minus the two sides of each rep by x
6000-240x-100x+4x^2=4200
4x^2-240x-100x+6000-4200=
4x^2-340x+1800=0
4(x-5)(x-90)
this is where x should equal the width of the border, but 5 does not work, what am I doing wrong?
Answer by jim_thompson5910(35256) About Me  (Show Source):
You can put this solution on YOUR website!
Assuming that the problem has the correct numbers (ie there are no typos in the book), you're doing great until you reach the point where you try to factor. It turns out that 4x%5E2-340x%2B1800 can't be factored at all (over the rationals). So we must use the quadratic formula to solve



4x%5E2-340x%2B1800=0 Start with the given equation.


Notice that the quadratic 4x%5E2-340x%2B1800 is in the form of Ax%5E2%2BBx%2BC where A=4, B=-340, and C=1800


Let's use the quadratic formula to solve for "x":


x+=+%28-B+%2B-+sqrt%28+B%5E2-4AC+%29%29%2F%282A%29 Start with the quadratic formula


x+=+%28-%28-340%29+%2B-+sqrt%28+%28-340%29%5E2-4%284%29%281800%29+%29%29%2F%282%284%29%29 Plug in A=4, B=-340, and C=1800


x+=+%28340+%2B-+sqrt%28+%28-340%29%5E2-4%284%29%281800%29+%29%29%2F%282%284%29%29 Negate -340 to get 340.


x+=+%28340+%2B-+sqrt%28+115600-4%284%29%281800%29+%29%29%2F%282%284%29%29 Square -340 to get 115600.


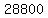
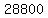x+=+%28340+%2B-+sqrt%28+115600-28800+%29%29%2F%282%284%29%29 Multiply 4%284%29%281800%29 to get 28800


x+=+%28340+%2B-+sqrt%28+86800+%29%29%2F%282%284%29%29 Subtract 28800 from 115600 to get 86800


x+=+%28340+%2B-+sqrt%28+86800+%29%29%2F%288%29 Multiply 2 and 4 to get 8.


x+=+%28340+%2B-+20%2Asqrt%28217%29%29%2F%288%29 Simplify the square root (note: If you need help with simplifying square roots, check out this solver)


x+=+%28340%2B20%2Asqrt%28217%29%29%2F%288%29 or x+=+%28340-20%2Asqrt%28217%29%29%2F%288%29 Break up the expression.


So the solutions are x+=+%28340%2B20%2Asqrt%28217%29%29%2F%288%29 or x+=+%28340-20%2Asqrt%28217%29%29%2F%288%29


which approximate to x=79.327 or x=5.673


However, take note that 50-2x=50-2%2879.327%29=-108.654 when x=79.327. So x=79.327 may be a solution, but it doesn't make sense in this problem since you can't have a negative width.


So the only value that makes sense is x=5.673


This means that the width of the border is about 5.673 yards. Normally, you'd get a clean number. It's not guaranteed, but books tend to fix problems so nice solutions result. So I'd double check the problem.