SOLUTION: if one painter can paint a house in 6 hours, and another painter paints a house in 9 hours. How long will it take them to paint the house working together

Click here to see ALL problems on Proportions

Question 249470: if one painter can paint a house in 6 hours, and another painter paints a house in 9 hours. How long will it take them to paint the house working together
Found 2 solutions by oberobic, Edwin McCravy:
Answer by oberobic(2304) (Show Source):
You can put this solution on YOUR website!
The key to solving "job" problems is to realize the job is 1 whole job that is divided into components that people do at different rates.
.
One painter paints the house in 6 hours, so his rate is 1/6 of the house per hour.
The other painter takes 9 hrs, so his rate is 1/9 of the house per hour.
.
Since we are not told otherwise, we assume they are working simultaneously: we assume they start and stop at the same time. So each of them works the same amount of time, which we will call 'x' hours.
.
First we set up time/rate for both painters: painter 1 works 'x' hrs at 1/6 of the whole job per hr; painter two works 'x' hrs at 1/9 of the whole job per hr:

.
The least common denominator is 54:

.
Cross multiply

.
Divide both sides by 15

Working together it takes them 3.6 hrs to paint the house.
.
Check by substituting back into the painter's rates to see if they total 1.

So working together they complete 1 whole job in 3.6 hr = 3 hr 36 min = 216 minutes, depending on the units the answer should be in.
.
Done.

Answer by Edwin McCravy(20064) (Show Source):
You can put this solution on YOUR website!
if one painter can paint a house in 6 hours, and another painter paints a house in 9 hours. How long will it take them to paint the house working together

Let x = the number of hours working together (what is asked for) Make this chart: No. of Houses Rate Time first painter second painter ------------------------------------------------------ both together Fill in x for the time for both together to paint 1 house: No. of Houses Rate Time first painter second painter ------------------------------------------------------ both together 1 x

>>...one painter can paint a house in 6 hours...<<

So fill in 1 house and 6 hours for the first painter, his no. of houses and his number of hours, respectively. No. of Houses Rate Time first painter 1 6 second painter ------------------------------------------------------ both together 1 x

>>...another painter paints a house in 9 hours...<<

So fill in 1 house and 9 hours for the second painter, his no. of houses and his number of hours, respectively. No. of Houses Rate Time first painter 1 6 second painter 1 9 ------------------------------------------------------ both together 1 x Now fill in all three rates using the formula No. of Houses Rate Time first painter 1 1/6 6 second painter 1 1/9 9 ------------------------------------------------------ both together 1 1/x x Now form the equation by using the fact that First painter's rate + Second painter's rate = their rate together Can you get a LCD of 18x and solve that equation for x? If not post again asking how to. Answer: hours or hours or 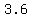hours or hours and minutes. Edwin