Question 24636: Could you please help me with this problem
Use f(x)=4x to the -5 power and g(x)= x to the 3/4 power
f(g(x))
and g(f(x))
Answer by longjonsilver(2297)   (Show Source): (Show Source):
You can put this solution on YOUR website! You do not say whether f(x) is 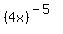 or or  . I shall take the latter, since that is what you wrote, although you may not have meant it. . I shall take the latter, since that is what you wrote, although you may not have meant it.
f(x) = 
g(x) = 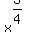
Now functions are so easy, it is unbelievable that students struggle...bad teaching perhaps? :-)
ANY function will be written like h(a) = something. All this means is put the value in the bracket, here a, into the "something". This is ALL you do.
So, fg(x) says put the value of x into g first....ok doing this gives f(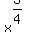 ) )
Now we have to do the function f. The definition of function f says, whatever is in the bracket, you raise to the power -5 and then multiply by 4. OK then, we have 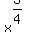 as our "x", so lets do that: as our "x", so lets do that:
f(x) =  . Now the question doesn't say simplify it, so you could leave it like that. It is correct. Or perhaps combine the 2 powers, giving f(x) = . Now the question doesn't say simplify it, so you could leave it like that. It is correct. Or perhaps combine the 2 powers, giving f(x) = 
OK, now for gf(x). Again, we will put the variable in the bracket (x) into function f first. We then put what is in the bracket into function g. That is ALL it is asking you do.
so, gf(x) -->  . .
and now, this becomes 
Again, we could try to simplify this one, but i don't think trying to do that will give you anything of benefit.
Is this clearer now?
Have a look at my Lesson on functions on this website...it explains this topic.
jon.
|
|
|