Question 246223: how do I solve: 3^(2X)-15(3^X)+56=0?
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! 
There are a couple of keys to solving this one:- Seeing
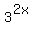 and and 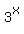 and realizing that and realizing that  . (If you don't see this, remember the property: . (If you don't see this, remember the property:  . If q=2 then . If q=2 then  . This tells us that any expression with an exponent that is a multiple of 2 is a perfect square and it is the prefect square of the expression with an exponent 1/2 as large. For example: . This tells us that any expression with an exponent that is a multiple of 2 is a perfect square and it is the prefect square of the expression with an exponent 1/2 as large. For example:  , ,  , etc.) , etc.) - Once we realize that
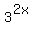 is the square of is the square of 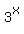 , then there is chance that you will notice that the equation is in quadratic form for , then there is chance that you will notice that the equation is in quadratic form for 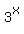 . If we use a temporary variable it will be easier to see this: . If we use a temporary variable it will be easier to see this:
Let  . Then . Then  and our equation becomes: and our equation becomes:

which is obviously a quadratic equation.
Once we see that this is a quadratic equation a solution becomes possible: Solve the quadratic equation and this will tell us what 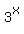 can be. Then we can use logarithms to find x. can be. Then we can use logarithms to find x.
It is faster but not as easy to see if you skip the temporary variable. I'll show you both solutions to the quadratic equation, with and without the temporary variable.
With the temporary variable.

Factor:

Use the Zero Product Property which tells us that this product can be zero only if one of the factors is zero. So:
 or or 
Solving these we get:
 or or 
Now we replace the temporary variable (because we no longer need it):
 or or 
Without the temporary variable. (Compare this with the solution above to understand it better.)

Factor:

Zero Product Property:
 or or 
Either with or without the temporary variable, we get to the following equations:
 or or 
We can use logarithms to solve them. It does not matter which base logarithm you use. But if you want a decimal approximation of the answer, then you should choose a base that your calculator "knows" how to find. I'll choose base 10 (base e (aka natural) logarithms would work just as well). Find the logarithm of both sides:
 or or 
Use a property of logarithms,  , to move the exponent of the argument in front. (This is why we use logarithms: To get the variable out of the exponent.) , to move the exponent of the argument in front. (This is why we use logarithms: To get the variable out of the exponent.)
 or or 
Divide both sides by 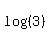 : :
 or or 
These are the exact solutions. If you want decimal approximations of them, just use your calculator to find the various logarithms and do the divisions.
|
|
|