|
Question 245944: I need some help!
square root of x+6 plus square root of 2-x=4
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! 
To solve equations with square roots, the general rule is:- Isolate a square root on one side of the equation.
- Square both sides.
- If there any any square roots remaining, repeat steps #1 and #2.
- Solve the equation (which, at this point, has no more square roots).
- Check you answer(s)!. This is more than just a good idea. It is important because whenever you square both sides of an equaiton, like we did in step #2, you may introduce what are called extraneous solutions. Extraneous solutions are solutions that, in this case, fit the squared equation but do not fit the original equation. Extraneous solutions must be rejected and the only waty to find them is to check your answers in the original equation.
So we start by isolating a square root. (It doesn't matter which one.) Adding 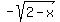 to each side we get: to each side we get:

Square both sides:

which simplifies to (be sure to use FOIL to square the right side):

which further simplifies to:

We still have a square root so we isolate it. Subtract 18 and add x to each side:

Square both sides:

Simplify:


We finally have an equation without square roots. Next we solve this equation. This is a quadratic equation so we'll get one side equal to zero by adding 64x and subtracting 128:

Next we either factor and use the Zero Product Property or use the Quadratic Formula. This factors pretty easily:



According to the Zero Product Property this (or any) product can be zero only if one of the factors is zero. 4 can't be zero but (x+2) could be zero. So we solve:
x+2 = 0
resulting in:
x = -2
Now, as was explained earlier, we must check out answer, using the original equation:

Checking x = -2:



 Check! Check!
|
|
|
| |