SOLUTION: Use the discriminant to determine whether the following equations have solutions that are: two different rational solutions; two different irrational solutions; exactly one rationa

Click here to see ALL problems on Equations

Question 245864: Use the discriminant to determine whether the following equations have solutions that are: two different rational solutions; two different irrational solutions; exactly one rational solution; or two different imaginary solutions.
25x^2 - 10x + 1 = 0
Found 2 solutions by solver91311, jsmallt9:
Answer by solver91311(24713) (Show Source):
You can put this solution on YOUR website!

The discriminant is the part of the quadratic formula under the radical, namely:

Two real and unequal roots. If is a perfect square, the roots are rational. Otherwise, they are irrational.

One real root with a multiplicity of two. That is to say that the trinomial is a perfect square and has two identical factors. The Fundamental Theorem of Algebra still holds because it allows counting roots up to the limits of their multiplicity.

A conjugate pair of complex roots of the form where is the imaginary number defined by

Terminology note: Rarely will you find a quadratic with purely imaginary roots. A quadratic that does not have real roots generally has complex number solutions which have a real part and an imaginary part. Hence, to say that a quadratic has "two different imaginary solutions" is almost always incorrect.

John

Answer by jsmallt9(3758) (Show Source):
You can put this solution on YOUR website!
The quadratic formula is:

The expression in the square root, , is called the discrimnant, because its value can be used to discriminate between the different types of solutions that are possible: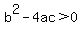
results in two real solutions
If is a perfect square (like 4, 9 64, 100, etc.) then you get two rational solutions.
If is a not perfect square then you get two irrational solutions.
If then you get a single real (and rational since 0 is a perfect square) solution.
If 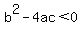then you get two complex solutions. (Note: you only get imaginary solutions if the discriminant is negative and b = 0!)

The logic behind all of this is:
Only zero has a single square root. Any other number will have two square roots, one positive and one negative.
The square roots of positive numbers are real (either rational or irrational).
The square roots of negative numbers are imaginary. And these imaginary roots, combined with the real number, the -b, in the numerator of the quadratic formula make the solutions complex (unless b = 0 in which case the solutions are pure imaginary numbers).

The discriminant of your equation

is

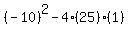
which simplifies to

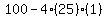
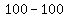
Since the discriminant of is 0, there will be a single rational root.