|
Question 245839: solve the system of inequalities y>x^2+1 over 2x-y>4
Answer by jsmallt9(3758)   (Show Source):
You can put this solution on YOUR website!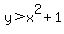 
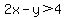
To graph the solution to a system of inequalities like this:- Graph the related equations except use dotted lines instead of solid lines for inequalities that do not have "or equal to".
- The dotted and/or solid lines from step #1 will divide the plane/page into separate regions. Shade in the correct region. To determine which region is correct:
- Use logic, or
- Use trial and error.
- Pick a point in one of the regions.
- See if that point fits both inequalities. If it does then that is the correct region to shade. If the point does not fit both inequliaites, try point(s) in a different regions until you find one that fits both inequalities
Note: Some regions will not be completely surrounded by dotted ot solid lines. These are infintiely large regions, which if one is the one to shade you just shade as much as you can. The shaded region plus the solid lines, if any, represent all the points whose coordinates fit both inequalities.
Your first equation is a parabola and should be fairly easy to graph. The second equation is a line. It is easier to graph if we get it into slope-intercept form. So we will subtract 2x from each side:
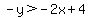
and divide both sides by -1 (remembering that whenever we divide both sides of an inequality by a negative that we need to reverse the inequality):
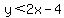
Since neither of the inequalities are of the "or equal to" type, we should draw both of these graphs with dotted lines.
Unfortunately Algebra.com's graphing software does not do inequalities or dotted lines so I cannot show you the solution. So here is a graph with solid lines, not the dotted lines we should use, of the two related equations:
As you can see the lines divide the plane into regions. Now we just have to figure out which region to shade:- Using logic at this point is easiest if both inequalities are solved for y. Fortunately both of these inequalities are already solved for y. The first one
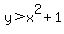
says that y is greater than 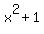 . Since larger y valus are up, we want a region that is above this parabola. The second one
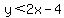
says that y is less than 2x-4. So we want a region that is below this line.
The solution to the system will be the region that is both above the parabola and below the line, at the same time. There is either one such region or none. If there are none, then there is no solution to the system. If there is a region that is both above the parabols and below the line then this is the region to shade. I hope from the graph above you can see that there is no place that is both above the parabola and below the line at the same time. There is no solution to this system. - If you use the trial and error method, then you would try a point from each region
- below the line (like (6, 0)
- a point between the line and the parabola (like (0, 0)
- a point inside the parabola (like (0, 5)
Be sure to pick points that are clearly in one region or another. In other words pick points that are not near any of the solid or dotted lines.
Now we try each point in both inequalities to see if it fits both. We should find that, for this system, that there are no points anywhere that fit both inequalities. (A point may fit one inequality or the other but not both.) So there is (still) no solution to this system.
|
|
|
| |
