Question 245559: The formula A = 201e0.021t models the population of a particular city, in thousands, t years after 1998. When will the population of the city reach 238 thousand?
Found 2 solutions by checkley77, jsmallt9:
Answer by checkley77(12844)   (Show Source):
You can put this solution on YOUR website! A = 201e0.021t
238=201*2.7184*.02t
238=10.928t
t=238/10.928
t=21.7789 number of years for the population to reach 238 thousand.
Answer by jsmallt9(3758) (Show Source):
You can put this solution on YOUR website! 
The problem is to find the value for t that makes A = 238.
To solve for a vairable in an exponent like this, we will generally use logarithms. But first, let's get rid of the number in front of the expnentiated expression. Divide both sides by 201:
Now we can use logartihms. Although any base logarithm can be used, it makes it easier if we use a base your calculator can do. Because of the "e" it is best to use base e (or natural, "ln") logarithms if your calculator can figure them out. (Most calculators which can do any logarithms can do base 10 and base e logarithms. I will use base e here but in case your calculator only does base 10, I will show that solution, too, at the end.)
Find the base e logarithm of each side:
Now we will use a property of logarithms,  , to move the exponent in the argument out in front of the loagarithm. (This is why we use logarithms. This property allows us to move the vaiable out of the exponent.)
Since  be definition we get:
Now all we have to do is divide by 0.021:
This is an exact answer. To get a more practical answer we can use our calculators:
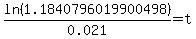
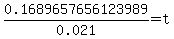
So approximately 8 years after 1998 (which is 2006), the population will be about 238 thousand.
If you calculator only does base 10:
(Note that log(e) is not 1 and does not "disappear" like ln(e) did above!) Divide both sides by  :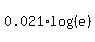
Now for the calculator work:
It was a little more difficult using base 10 instead of base e but note how we send up with the same answer. If our calculators could do base 14 we could have used that, too, and still we would get the same value for t!
|
|
|
