Question 244998: given log(base a)x=4, log(base a)y=3, and log(base a)z=2 for constants x, y,z. find the value of the logarithm.
log(base a)((5th root of y^3 times x^6 times z^4)/(5th root of z^6 times x^2)
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! you are given:
log(a,x) = 4
log(a,y) = 3
log(a,z) = 2
you want to find:
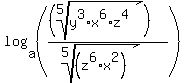
since  , your equation becomes: , your equation becomes:

since  , your equation becomes: , your equation becomes:
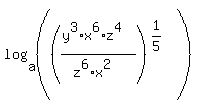
since log(a^b) = b*(log(a), your equation becomes:
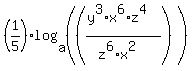
since log(a/b) = log(a)/log(b), your equation becomes:
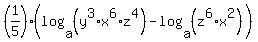
since log(a*b) = log(a) + log(b), your equation becomes:
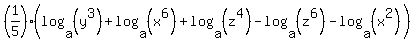
since log(a^b) = b*log(a), your equation becomes:
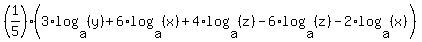
from here on it's just a straight substitution since you are given:
log(a,x) = 4
log(a,y) = 3
log(a,z) = 2
your equation of:
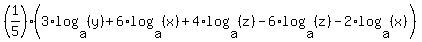
becomes:
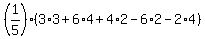 which becomes: which becomes:
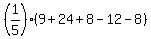 which becomes: which becomes:
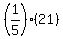 which becomes: which becomes:
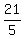
|
|
|