Question 244998: given log(base a)x=4, log(base a)y=3, and log(base a)z=2 for constants x, y,z. find the value of the logarithm.
log(base a)((5th root of y^3 times x^6 times z^4)/(5th root of z^6 times x^2)
Found 4 solutions by Theo, MathTherapy, CPhill, n2:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! you are given:
log(a,x) = 4
log(a,y) = 3
log(a,z) = 2
you want to find:
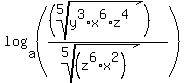
since  , your equation becomes: , your equation becomes:

since  , your equation becomes: , your equation becomes:
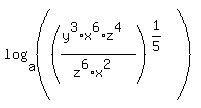
since log(a^b) = b*(log(a), your equation becomes:
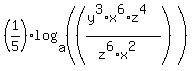
since log(a/b) = log(a)/log(b), your equation becomes:
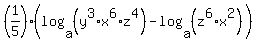
since log(a*b) = log(a) + log(b), your equation becomes:
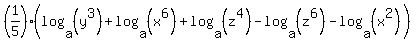
since log(a^b) = b*log(a), your equation becomes:
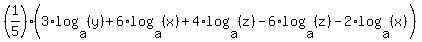
from here on it's just a straight substitution since you are given:
log(a,x) = 4
log(a,y) = 3
log(a,z) = 2
your equation of:
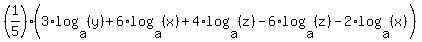
becomes:
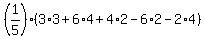 which becomes: which becomes:
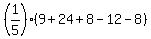 which becomes: which becomes:
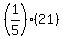 which becomes: which becomes:
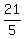
Answer by MathTherapy(10699)   (Show Source): (Show Source):
Answer by CPhill(2189)   (Show Source): (Show Source):
You can put this solution on YOUR website! To find the value of the logarithmic expression, we use the properties of logarithms to expand and simplify the expression into terms we already know.
### Given:
1.
2.
3.
### Expression to find:
---
### Step 1: Simplify the expression inside the logarithm
Using the laws of exponents ( and ):
* For :
* For :
* For :
The expression simplifies to:
---
### Step 2: Use Logarithm Rules to expand
Applying the product rule () and the power rule ():
---
### Step 3: Substitute the given values
Substitute , , and :
Combine the fractions:
Convert to decimal form:
**Final Answer:**
The value of the logarithm is **23.4**.
Answer by n2(36)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
I checked the solution by @MathTherapy to this problem, and I confirm that his solution and his answer
to this problem 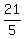 = 4 = 4 = 4.2 are correct. = 4.2 are correct.
The final answer 23.4 in the post by @CPhill is INCORRECT.
In addition, the post by @CPhill is absolutely inappropriate due to its form, since critically important
calculations are intentionally omitted. Such calculations should be presented explicitly -
without them, the post is a pure speculation.
More than strange a behavior of @CPhill at this forum.
I recommend to a reader to ignore the post by @CPhill.
|
|
|