Find the center and the radius of the circle described by the equation
 Get the term in
Get the term in  next to the term in
next to the term in  Get the term in
Get the term in  next to the term in
next to the term in  Add
Add  to both sides to get the constant on the right:
to both sides to get the constant on the right:
 Multiply the coefficient of
Multiply the coefficient of  , which is
, which is  by
by  ,
getting
,
getting  . Then square
. Then square  , getting
, getting  . Then add
. Then add
 to both sides, writing it next to the term in
to both sides, writing it next to the term in  on
the left.
on
the left.
 Multiply the coefficient of
Multiply the coefficient of  , which is
, which is  by
by  ,
getting
,
getting  . Then square
. Then square  , getting
, getting  . Then add
. Then add
 to both sides, writing it next to the term in
to both sides, writing it next to the term in  on
the left.
on
the left.
 Factor the first three terms on the left as a perfect square:
Factor the last three terms on the left as a perfect square:
Combine the numbers on the right side:
Factor the first three terms on the left as a perfect square:
Factor the last three terms on the left as a perfect square:
Combine the numbers on the right side:
 Compare that to the standard equation of a circle, which is:
Compare that to the standard equation of a circle, which is:
 where the center is
where the center is 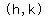 So
So  ,
,  ,
,  Therefore the center is the point
Therefore the center is the point  And since
And since
 , we take the square root of both sides,
and get
, we take the square root of both sides,
and get
 So the radius of the circle is
So the radius of the circle is  .
Edwin
.
Edwin