Question 243740: Please help me to figure out this problem:
THis is how the word problem is written in the book:
Find three consecutive even intergers such that the square of the largest exceeds the sum of the squares of the other two by 12.
Found 3 solutions by Alan3354, stanbon, oberobic:
Answer by Alan3354(69443)   (Show Source): (Show Source):
You can put this solution on YOUR website! Find three consecutive even intergers such that the square of the largest exceeds the sum of the squares of the other two by 12.
-------------
They're x, x+2 and x+4
(x+4)^2 = x^2 + (x+2)^2 + 12
-----------------------
Can you do the rest?
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! Find three consecutive even integers such that the square of the largest exceeds the sum of the squares of the other two by 12.
----------------------
1st: 2x
2nd: 2x+2
3rd: 2x+4
------------------
Equation:
(2x+4)^2 = (2x)^2 + (2x+2)^2 + 12
------------------------------------------
4x^2 + 16x + 16 = 4x^2 + 4x^2 + 8x + 4 + 12
4x^2-8x = 0
4x(x-2) = 0
x = 0 or x = 2
-----------------------
If x = 0
2x = 0
2x+2 = 2
2x+4 = 4
Check:
4^2 = 0^2 + 2^2 + 12
Good solution
-------------------------------
If x = 2
2x = 4
2x+2 = 6
2x+4 = 8
Check:
8^2 = 6^2 + 2^2 + 12
64 = 36 + 16
x=2 does not give a solution set.
===================================
Cheers,
Stan H.
Answer by oberobic(2304)   (Show Source): (Show Source):
You can put this solution on YOUR website! For most problems like this, your best interest is served by using as few variables as possible. For example, the setup says "3 consecutive EVEN integers," which is a temptation to call x, y, and z.
But from what we know about consecutive numbers, they're just 1 apart. Consecutive EVEN integers are 2 apart. So we can define the 3 unknown numbers in terms of x.
a = x
b = x+2
c = x+4
.
We're all told the square of the largest number 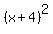 is 12 more than the sum of the squares of the other two numbers. We can write this fact as: is 12 more than the sum of the squares of the other two numbers. We can write this fact as: 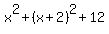 . Combining we have: . Combining we have:
.

.
Resolving the squares.



.
Collecting like terms
Subtract x^2 from both sides

Subtracting 8x from both sides

Subtracting 16 from both sides


.
We can factor an 'x' from the left-hand.

.
So we have two possible solutions:
x=0
x=4
.
Testing x=0.
0^2 = 0
2^2 = 4
4^2 = 16
Is 4^2 equal to the sum of the other two squares + 12?
Yes.
.
Testing x=4.
4^2 = 16
6^2 = 36
8^2 = 64
Is 8^2 equal to the sum of the other two squares + 12?
16+36=52, with is 12 less than 64.
So this works, too.
.
The EVEN consecutive digits are:
0, 2 & 4
and
4, 6 & 8
.
Done.
|
|
|