Find two positive numbers such the sum of the first and twice the second is 100 and their product is as large as possible?
Let t = the first number
Let x = the second number
>>...the sum of the first and twice the second is 100...<<
We want to maximize the product xy.
Let y = the product = tx
Solve for t
Substitute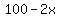 
for t in
If you are taking algebra, not calculus, then find the
vertex of the parabola
Since the coefficient of 
is negative, the
graph opens downward and thus reaches a maximum at the
vertex.
The formula for the x-coordinate of the vertex = 
So the x-coordinate of the vertex is 
So the value of x is 25
Now substitute 25 for x in
So the two numbers are
first = 25
second = 50
---------------------------------------------
If you're taking calculus, you would do it by
taking the derivative of
and set the derivative = 0
and as in the algebra way, 
Edwin
