SOLUTION: The sum of the digits of a three-digit number is 6. If the hundreds and tens are reversed, the resulting number is 90 more than the original number.If the tens and units digits are

Algebra ->  Customizable Word Problem Solvers  -> Misc -> SOLUTION: The sum of the digits of a three-digit number is 6. If the hundreds and tens are reversed, the resulting number is 90 more than the original number.If the tens and units digits are      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 242911: The sum of the digits of a three-digit number is 6. If the hundreds and tens are reversed, the resulting number is 90 more than the original number.If the tens and units digits are reversed,the resulting number is 9 more than the original number. Find the original number
Answer by Edwin McCravy(20064) About Me  (Show Source):
You can put this solution on YOUR website!
The sum of the digits of a three-digit number is 6. If the hundreds and tens are reversed, the resulting number is 90 more than the original number.If the tens and units digits are reversed,the resulting number is 9 more than the original number. Find the original number

Let h = the hundreds digit
Let t = the tens digit
Let u = the units digit

Then the original number = 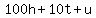100h+%2B+10t+%2B+u
The number formed by reversing the hundreds and tens digits = 100t%2B10h%2Bu
The number formed by reversing the tens and units digits = 100h%2B10u%2Bt
The sum of the digits of a three-digit number is 6.

That says:

h+%2B+t+%2B+u+=+6

If the hundreds and tens are reversed, the
resulting number is 90 more than the original number

That says:

100t+%2B+10h+%2B+u+=+%28100h+%2B+10t+%2B+u%29+%2B+90

Simplifying:

100t+%2B+10h+%2B+u+=+100h+%2B+10t+%2B+u+%2B+90
90t+-+90h+=+90
t+-+h+=+1

If the tens and units digits are reversed,the resulting number is 9 more than the original number. 

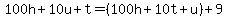
100h+%2B+10u+%2B+t+=+%28100h+%2B+10t+%2B+u%29+%2B+9
100h+%2B+10u+%2B+t+=+100h+%2B+10t+%2B+u+%2B+9
9u+-+9t+=+9
u+-+t+=+1

Simplifying:

system%28h+%2B+t+%2B+u+=+6%2Ct-h=1%2Cu+-+t+=+1%29

Solve that and get h=1, t=2, u=3.

So the original number = 123

Checking:

The original number = 123
The number formed by reversing the hundreds and tens digits = 213
The number formed by reversing the tens and units digits = 132.

The sum of the digits of a three-digit number is 6. 

1+2+3=6 That checks.

If the hundreds and tens are reversed, the resulting number is 90 more than the original number.

213 is 90 more than 123.  That checks

If the tens and units digits are reversed,the resulting number is 9 more than the original number

132 is 9 more than 123. That checks.
 
So it's correct.  The original number is 123.

Edwin