Question 242739: A local paper reports that the average number of representatives per night at a local hotel is 500. Using alpha = .01 is this claim realistic? Use the given hotels reservations listed below: 713 300 292 311 598 401 618
Found 2 solutions by stanbon, Edwin McCravy:
Answer by stanbon(75887)   (Show Source):
You can put this solution on YOUR website! A local paper reports that the average number of representatives per night at a local hotel is 500. Using alpha = .01 is this claim realistic? Use the given hotels reservations listed below: 713 300 292 311 598 401 618
------------
Ho: u = 500
H1: u is not 500
----------------------
sample mean = 240.5 ; sample std = 120.59
-----------------------
CV for 2-tail test, alpha = 1%, df = 6: t = -3.707
TS: t(240.5) = (240.5-500)/[120.59/sqrt(7)] = -5.693
Since the ts is in the reject interval, reject Ho.
Looks like the average number is lower than 500.
Cheers,
Stan H.
Answer by Edwin McCravy(20060)  (Show Source):
You can put this solution on YOUR website! The other tutor's answer is incorrect.
A local paper reports that the average number of representatives per night at a local hotel is 500. Using alpha = .01 is this claim realistic? Use the given hotels reservations listed below: 713 300 292 311 598 401 618
  
 
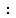
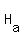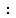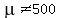This is a two-tail t-test. It's a t-test, not a z-test because
only a small sample is given. It's a two-tail test because nothing
is said about whether it is being challenged as being either greater
than 500 or less than 500, but just that it is being challenged
as possibly not equal to 500.
Let's begin by finding the rejection region:
Since this is a two tail test, the area in each tail is
half of  so we look under the column for
.005 in the right tail, and use 7-1 or 6 degrees of freedom,
since there are 7 statistics in the data. We read there 3.707.
Now we must calculate the test statistic, t. If t is either
greater than 3.707 or less than -3.707, then we will have
sufficient evidence to reject the null huypothesis, otherwise
we cannot reject the null hypothesis that .
Calculate:
_
x = 461.8571429
s = 176.7761565
I assume you can do this. If you can't, post again asking how.
Calculate the test statistic:
So t does not fall in the rejection region, so this data does not
furnish us with enough evidence to reject .
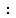So we will have to say the claim is realistic.
Edwin
|
|
|
