SOLUTION: Find a polynomial function of degree 3 with -2, and 7i as zeros.

Algebra ->  Functions -> SOLUTION: Find a polynomial function of degree 3 with -2, and 7i as zeros.      Log On


   

Question 240795: Find a polynomial function of degree 3 with -2, and 7i as zeros.
Found 3 solutions by vleith, jsmallt9, stanbon:
Answer by vleith(2983) About Me  (Show Source):
You can put this solution on YOUR website!
You know that roots result in zeros.
So a zero at x=-2 means (x+2) is a factor in the formula for the polynomial.
Likewise you are told you have an imaginary root at 7i. You know that imaginary roots come in pairs (7i , -7i)
So two more factors are (x-7i) and (x+7i)
Now you have three terms. The polynomial is the product of those three factors.
p%28y%29+=+%28x%2B2%29%28x%2B7i%29%28x-7i%29
p%28y%29+=+%28x%2B2%29%28x%5E2-49i%5E2%29
p%28y%29+=+%28x%2B2%29%28x%5E2%2B49%29
All you need to do now is simplify by multiplying it all out. I'll leave that to you, because I know you can do that. Ping me if you need more help

Answer by jsmallt9(3758) About Me  (Show Source):
You can put this solution on YOUR website!
In general a polynomial function with zeros of z%5B1%5D, z%5B2%5D, z%5B3%5D, ... , z%5Bn%5D will have an equation of the form:
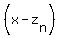
f%28x%29+=+%28x+-+z%5B1%5D%29%28x+-+z%5B2%5D%29%28x+-+z%5B3%5D%29...%28x-z%5Bn%5D%29

So if we know all the zeros of the polynomial then we will be able to find the polynomial. You are given two zeros but a polynomial of degree 3 should have 3 zeros. we need the third zero. The key is to understand when a zero is complex or imaginary, like 7i, then its conjugate, -7i, will also be a zero. So we now have our three zeros: -2, 7i and -7i.

With these zeros we can write the equation:
f%28x%29+=+%28x+-+%28-2%29%29%28x+-+7i%29%28x+-+%28-7i%29%29
All that is left is to simplify. First we'll write the "minus a negatives" as additions of positives:
f%28x%29+=+%28x+%2B+2%29%28x+-+7i%29%28x+%2B+7i%29
Now we'll multiply it out. It is easiest if we multiply the last two factors first because they fit the pattern %28a%2Bb%29%28a-b%29+=+a%5E2-b%5E2 and because we want to get rid of the i's ASAP:
f%28x%29+=+%28x%2B2%29%28x%5E2+-+%287i%29%5E2%29
Since %287i%29%5E2+=+%287i%29%287i%29+=+7%2A7%2Ai%2Ai+=+49i%5E2 and since i%5E2+=+-1, we get:
f%28x%29+=+%28x%2B2%29%28x%5E2+-+%28-49%29%29+=+%28x%2B2%29%28x%5E2+%2B+49%29
And after the last multiplication we get:
f%28x%29+=+x%5E3+%2B+2x%5E2+%2B+49x+%2B+98

Answer by stanbon(75887) About Me  (Show Source):
You can put this solution on YOUR website!
Find a polynomial function of degree 3 with -2, and 7i as zeros.
----------------
If the polynomial function must have Real Number coefficients,
-7i must also be a zero.
-----------------------------
f(x) = (x-3)(x-7i)(x+7i)
f(x) = (x-3)(x^2+49)
f(x) + x^3-3x^2+49x-147
=============================
Cheers,
Stan H.