Question 240665: Express in logarithmic form of 64½=8
Found 2 solutions by jsmallt9, Theo:
Answer by jsmallt9(3758)   (Show Source):
Answer by Theo(13342)  (Show Source):
You can put this solution on YOUR website! The definition of logarithms states:
log(b,x) = y if and only if b^y = x
and:
b^y = x if and only if log(b,x) = y
Since 1/2 = .5, your formula becomes:
64^(.5) = 8
If we let:
64 = b
.5 = y
8 = x
Then, the definition of logarithms applied to your formula states:
64^(.5) = 8 if and only if log(64,8) = .5.
Algebra.com formula generator make it look like this:
 if and only if 
If you put 64^(.5) in your calculator, you will get 8.
If you put log(8)/log(64) in your calculator, you will get .5
log(8)/log(64) is equivalent to 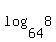 which means log of 8 to the base of 64.
The procedure uses the change of base of logarithm formula of:
This formula states that if you have a logarithm of a number to the base of b, and you want to convert it to a logarithm of the same number to the base of c, you take the logarithm of the number to the base of c and you divide it by the logarithm of the base of b to the base of c.
In your problem, we converted your exponential equation to the logarithmic form to get:
log of 8 to the base of 64 = .5
to prove that was true using the calculator, we had to convert the logarithm to the base of 64 to a logarithm to the base of 10 because the LOG function of the calculator works to the base of 10.
The formula we used was the change of base formula.
We took the logarithm of 8 to the base of 64 and converted it to the logarithm of 8 to the base as shown below:
log of 8 to the base of 64 = log of 8 to the base of 10 divided by the log of 64 to the base of 10.
this became:
 making the result = .5
|
|
|
